Точки Лагранжа

Точки Лагранжа и эквипотенциальные поверхности системы двух тел (с учётом центробежного потенциала)

Точки Лагранжа, точки либрации (librātiō — раскачивание) или L-точки — точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, не испытывающее воздействие никаких других сил, кроме гравитационных, со стороны двух первых тел, может оставаться неподвижным относительно этих тел.

Более точно точки Лагранжа представляют собой частный случай при решении так называемой ограниченной задачи трёх тел — когда орбиты всех тел являются круговыми и масса одного из них намного меньше массы любого из двух других. В этом случае можно считать, что два массивных тела обращаются вокруг их общего центра масс с постоянной угловой скоростью. В пространстве вокруг них существуют пять точек, в которых третье тело с пренебрежимо малой массой может оставаться неподвижным во вращающейся системе отсчёта, связанной с массивными телами. В этих точках гравитационные силы, действующие на малое тело, уравновешиваются центробежной силой.

Точки Лагранжа получили своё название в честь математика Жозефа Луи Лагранжа, который первым в 1772 году привёл решение математической задачи, из которого следовало существование этих особых точек.

Расположение точек Лагранжа

Схема пяти лагранжевых точек в системе двух тел, когда одно тело намного массивнее другого (Солнце и Земля). В такой системе точки L3, L4, L5 показаны на самой орбите, хотя фактически они будут находиться немного за ней

Все точки Лагранжа лежат в плоскости орбит массивных тел и обозначаются заглавной латинской буквой L с числовым индексом от 1 до 5. Первые три точки расположены на линии, проходящей через оба массивных тела. Эти точки Лагранжа называются коллинеарными и обозначаются L1, L2 и L3. Точки L4 и L5 называются треугольными или троянскими.

L1 находится между двумя телами системы, ближе к менее массивному телу, L2 — снаружи, за менее массивным телом и L3 — за более массивным. Расстояния от центра масс системы до этих точек в первом приближении по α рассчитываются с помощью следующих формул:

,

R — расстояние между телами, M1 — масса более массивного тела, M2 — масса второго тела.

L1

Точка L1 лежит на прямой, соединяющей два тела с массами M1 и M2 (M1 > M2), и находится между ними, вблизи второго тела. Её наличие обусловлено тем, что гравитация тела M2 частично компенсирует гравитацию тела M1. При этом чем больше M2, тем дальше от него будет располагаться эта точка.

Пример: Объекты, которые движутся вокруг Солнца ближе, чем Земля, как правило, имеют меньшие орбитальные периоды, чем у Земли, если они не входят в зону влияния земного притяжения. Если объект находится непосредственно между Землёй и Солнцем, то действие земной силы тяжести отчасти компенсирует влияние гравитации Солнца, за счёт этого происходит увеличение орбитального периода объекта. Причём чем ближе к Земле находится объект, тем сильнее этот эффект. И наконец, на определённом приближении к планете — в точке L1 — действие земной силы тяжести уравновешивает влияние солнечной гравитации настолько, что период обращения объекта вокруг Солнца становится равным периоду обращения Земли. Для нашей планеты расстояние до точки L1 составляет около 1,5 млн км. Притяжение Солнца здесь (118 мкм/с²) на 2 % сильнее, чем на орбите Земли (116 мкм/с²), тогда как снижение требуемой центростремительной силы вдвое меньше (59 мкм/с²). Сумма этих двух эффектов уравновешивается притяжением Земли, которое составляет здесь также 177 мкм/с². Использование

В системе Солнце—Земля точка L1 может быть идеальным местом для размещения космической обсерватории для наблюдения Солнца, которое в этом месте никогда не перекрывается ни Землёй, ни Луной. Первым космическим аппаратом, работавшим вблизи этой точки, был запущенный в августе 1978 года аппарат ISEE-3. Аппарат вышел на периодическую гало-орбиту вокруг этой точки 20 ноября 1978 года и был сведён с этой орбиты 10 июня 1982 года (для исполнения новых задач). На такой же орбите с мая 1996 года работает аппарат SOHO. Аппараты ACE, WIND и DSCOVR находятся на квази-периодических орбитах Лиссажу́ близ этой же точки, соответственно, с 12 декабря 1997, 16 ноября 2001 и 8 июня 2015 года.

Лунная точка L1 (в системе Земля — Луна) может стать идеальным местом для строительства космической пилотируемой орбитальной станции, которая, располагаясь на «полпути» между Землёй и Луной, позволила бы легко добраться до Луны с минимальными затратами топлива и стать ключевым узлом грузового потока между Землёй и её спутником.

L2

Точка L2 в системе Солнце — Земля, располагающаяся далеко за пределами орбиты Луны

Точка L2 лежит на прямой, соединяющей два тела с массами M1 и M2 (M1 > M2), и находится за телом с меньшей массой. Точки L1 и L2 располагаются на одной линии и в пределе M1 ≫ M2 симметричны относительно M2. В точке L2гравитационные силы, действующие на тело, компенсируют действие центробежных сил во вращающейся системе отсчёта.

Пример: у объектов, расположенных за орбитой Земли, орбитальный период почти всегда больше, чем у Земли. Но дополнительное влияние на объект силы тяжести Земли, помимо действия солнечной гравитации, приводит к увеличению скорости вращения и уменьшению времени оборота вокруг Солнца, в результате в точке L2орбитальный период объекта становится равным орбитальному периоду Земли.

Точка L2 в системе Солнце — Земля является идеальным местом для строительства орбитальных космических обсерваторий и телескопов. Поскольку объект в точке L2 способен длительное время сохранять свою ориентацию относительно Солнца и Земли, производить его экранирование и калибровку становится гораздо проще. Однако эта точка расположена немного дальше земной тени (в области полутени), так что солнечная радиация блокируется не полностью. В этой точке уже находятся аппараты американского и европейского космических агентств — WMAP, «Планк», «Гершель» и “Gaia”, а в 2018 должен присоединиться «Джеймс Уэбб». Точка L2 в системе Земля—Луна может быть использована для обеспечения спутниковой связи с объектами на обратной стороне Луны, а также быть удобным местом для размещения заправочной станции для обеспечения грузопотока между Землёй и Луной.

Если M2 много меньше по массе, чем M1, то точки L1 и L2 находятся на примерно одинаковом расстоянии r от тела M2, равном радиусу сферы Хилла :

где R — расстояние между компонентами системы.

Это расстояние можно описать как радиус круговой орбиты вокруг M2, для которой период обращения в отсутствие M1 в раз меньше, чем период обращения M2 вокруг M1.

Примеры

• В системе Солнце — Земля: 1 500 000 км от Земли
• Земля — Луна: 61 500 км от Луны

L3

Три из пяти точек Лагранжа расположены на одной оси, соединяющей два тела

Точка L3 лежит на прямой, соединяющей два тела с массами M1 и M2 (M1 > M2), и находится за телом с большей массой. Так же, как для точки L2, в этой точке гравитационные силы компенсируют действие центробежных сил.

Пример: Точка L3 в системе Солнце — Земля находится за Солнцем, на противоположной стороне земной орбиты. Однако, несмотря на свою небольшую гравитацию (по сравнению с гравитацией Солнца), Земля всё же оказывает на него небольшое влияние, поэтому точка L3 находится не на самой орбите Земли, а чуть дальше от Солнца, чем Земля, так как вращение происходит не вокруг Солнца, а вокруг барицентра). В результате в этой точке L3 достигается такое сочетание гравитации Солнца и Земли, что объекты, находящиеся в этой точке, движутся с таким же орбитальным периодом, как и наша планета.

До начала космической эры среди писателей-фантастов была очень популярна идея о существовании на противоположной стороне земной орбиты в точке L3 другой аналогичной ей планеты, называемой «Противоземлёй», которая из-за своего расположения была недоступна для прямых наблюдений. Однако на самом деле из-за гравитационного влияния других планет точка L3 в системе Солнце — Земля является крайне неустойчивой. Так, во время гелиоцентрических соединений Земли и Венеры по разные стороны Солнца, которые случаются каждые 20 месяцев, Венера находится всего в 0,3 а. е. от точки L3 и таким образом оказывает очень серьёзное влияние на её расположение относительно земной орбиты. Кроме того, из-за несбалансированности центра тяжести системы Солнце — Юпитер относительно Земли и эллиптичности земной орбиты, так называемая «Противоземля» всё равно время от времени была бы доступна для наблюдений и обязательно была бы замечена. Ещё одним эффектом, выдающим её существование, была бы её собственная гравитация: влияние тела размером уже порядка 150 км и более на орбиты других планет было бы заметно. С появлением возможности производить наблюдения с помощью космических аппаратов и зондов было достоверно показано, что в этой точке нет объектов размером более 100 м.

Орбитальные космические аппараты и спутники, расположенные вблизи точки L3, могут постоянно следить за различными формами активности на поверхности Солнца, в частности, о появлении новых пятен или вспышек, и оперативно передавать информацию на Землю (например, в рамках системы раннего предупреждения о космической погоде NOAA Space Weather Prediction Center). Кроме того, информация с таких спутников может быть использована для обеспечения безопасности дальних пилотируемых полётов, например к Марсу или астероидам. В 2010 году были изучены несколько вариантов запуска подобного спутника.

L4 и L5

Гравитационное ускорение в точке L4

Если на основе линии, соединяющей оба тела системы, построить два равносторонних треугольника, две вершины которых соответствуют центрам тел M1 и M2, то точки L4 и L5 будут соответствовать положению третьих вершин этих треугольников, расположенных в плоскости орбиты второго тела в 60 градусах впереди и позади него.

Наличие этих точек и их высокая стабильность обусловливается тем, что, поскольку расстояния до двух тел в этих точках одинаковы, то силы притяжения со стороны двух массивных тел соотносятся в той же пропорции, что их массы, и таким образом результирующая сила направлена на центр масс системы; кроме того, геометрия треугольника сил подтверждает, что результирующее ускорение связано с расстоянием до центра масс той же пропорцией, что и для двух массивных тел. Так как центр масс является одновременно и центром вращения системы, результирующая сила точно соответствует той, которая нужна для удержания тела в точке Лагранжа в орбитальном равновесии с остальной системой. (На самом деле, масса третьего тела и не должна быть пренебрежимо малой). Данная треугольная конфигурация была обнаружена Лагранжем во время работы над задачей трёх тел. Точки L4 и L5 называют треугольными (в отличие от коллинеарных).

Также точки называют троянскими: это название происходит от троянских астероидов Юпитера, которые являются самым ярким примером проявления этих точек. Они были названы в честь героев Троянской войны из «Илиады» Гомера, причём астероиды в точке L4 получают имена греков, а в точке L5 — защитников Трои; поэтому их теперь так и называют «греками» (или «ахейцами») и «троянцами».

Расстояния от центра масс системы до этих точек в координатной системе с центром координат в центре масс системы рассчитываются по следующим формулам:

где

, R — расстояние между телами, M1 — масса более массивного тела, M2 — масса второго тела.

• В 2010 году в системе Солнце — Земля в троянской точке L4 обнаружен астероид. В L5 пока не обнаружено троянских астероидов, но там наблюдается довольно большое скопление межпланетной пыли.
• По некоторым наблюдениям, в точках L4 и L5 системы Земля — Луна находятся очень разрежённые скопления межпланетной пыли — облака Кордылевского.
• В системе Солнце — Юпитер в окрестностях точек L4 и L5 находятся так называемые троянские астероиды. По состоянию на 21 октября 2010 известно около четырёх с половиной тысяч астероидов в точках L4 и L5.
• Троянские астероиды в точках L4 и L5 есть не только у Юпитера, но и у других планет-гигантов.
• Другим интересным примером является спутник Сатурна Тефия, в точках L4 и L5 которой находятся два небольших спутника — Телесто и Калипсо. Ещё одна пара спутников известна в системе Сатурн — Диона: Елена в точке L4 и Полидевк в точке L5. Тефия и Диона в сотни раз массивнее своих «подопечных», и гораздо легче Сатурна, что делает систему стабильной.
• Один из сценариев модели ударного формирования Луны предполагает, что гипотетическая протопланета (планетезималь) Тейя, в результате столкновения которой с Землёй образовалась Луна, сформировалась в точке Лагранжа L4 или L5 системы Солнце — Земля.
• Первоначально считалось, что в системе KOI-730 две из четырёх планет обращаются вокруг своего солнца по одной орбите. Вдоль общей орбиты эти два мира постоянно разделяют 60 градусов дистанции. Однако дальнейшие исследования показали, что данная система не содержит коорбитальных планет.

Равновесие в точках Лагранжа

Изображение двойной звезды Мира (омикрон Кита), сделанное космическим телескопом «Хаббл» в ультрафиолетовом диапазоне. На фотографии виден поток материи, направленный от основного компонента — красного гиганта — к компаньону — белому карлику. Массообмен осуществляется через окрестности точки L1

Тела, помещённые в коллинеарных точках Лагранжа, находятся в неустойчивом равновесии. Например, если объект в точке L1 слегка смещается вдоль прямой, соединяющей два массивных тела, сила, притягивающая его к тому телу, к которому оно приближается, увеличивается, а сила притяжения со стороны другого тела, наоборот, уменьшается. В результате объект будет всё больше удаляться от положения равновесия.

Такая особенность поведения тел в окрестностях точки L1 играет важную роль в тесных двойных звёздных системах. Полости Роша компонент таких систем соприкасаются в точке L1, поэтому, когда одна из звёзд-компаньонов в процессе эволюции заполняет свою полость Роша, вещество перетекает с одной звезды на другую именно через окрестности точки Лагранжа L1.

Несмотря на это, существуют стабильные замкнутые орбиты (во вращающейся системе координат) вокруг коллинеарных точек либрации, по крайней мере, в случае задачи трёх тел. Если на движение влияют и другие тела (как это происходит в Солнечной системе), вместо замкнутых орбит объект будет двигаться по квазипериодическим орбитам, имеющим форму фигур Лиссажу. Несмотря на неустойчивость такой орбиты, космический аппарат может оставаться на ней в течение длительного времени, затрачивая относительно небольшое количество топлива.

В отличие от коллинеарных точек либрации, в троянских точках обеспечивается устойчивое равновесие, если M1/M2 > 24,96. При смещении объекта возникают силы Кориолиса, которые искривляют траекторию, и объект движется по устойчивой орбите вокруг точки либрации.

Практическое применение

Полости Роша для двойной звёздной системы (обозначены жёлтым)

Исследователи в области космонавтики давно уже обратили внимание на точки Лагранжа. Например, в точке L1 системы Земля — Солнце удобно разместить космическую солнечную обсерваторию — она никогда не будет попадать в тень Земли, а значит, наблюдения могут вестись непрерывно. Точка L2 подходит для космического телескопа — здесь Земля почти полностью заслоняет солнечный свет, да и сама не мешает наблюдениям, поскольку обращена к L2 неосвещенной стороной. Точка L1 системы Земля — Луна удобна для размещения ретрансляционной станции в период освоения Луны. Она будет находиться в зоне прямой видимости для большей части обращённого к Земле полушария Луны, а для связи с ней понадобятся передатчики в десятки раз менее мощные, чем для связи с Землёй.

В настоящее время несколько космических аппаратов, в первую очередь, астрофизических обсерваторий, размещены или планируются к размещению в различных точках Лагранжа Солнечной системы:

Точка L1 системы Земля—Солнце:

• Космический аппарат WIND, предназначенный для исследования солнечного ветра (запущен в 1994 году).
• SOHO (Solar and Heliospheric Observatory, «Солнечная и гелиосферная обсерватория») (запущен в 1995 году).
• Advanced Composition Explorer (запущен в 1997 году).

Точка L2 системы Земля—Солнце:

• КА НАСА WMAP, изучающий реликтовое излучение (запущен в 2001 году).
• Космические телескопы «Гершель» и «Планк», (запущены в 2009 году).
• Европейский телескоп «Gaia» (запущен в 2013 году).
• Космический телескоп «Джеймс Уэбб», идущий на смену телескопу «Хаббл». Запуск планируется на 2018 год.
• В 2017 году НПО имени Лавочкина планирует разместить в точке L2 космическую обсерваторию Спектр-РГ.
• В 2024 году ЕКА планирует также разместить в точке L2 космический телескоп «PLATO».

Другие точки Лагранжа:

• в сентябре-октябре 2009 года два аппарата STEREO совершили транзит через точки L4 и L5.
• JIMO (Jupiter Icy Moons Orbiter) — отменённый проект НАСА по исследованию спутников Юпитера, который должен был активно использовать систему точек Лагранжа для перехода от одного спутника к другому с минимальными затратами топлива. Этот манёвр получил название «лестница Лагранжа».

Примечания

1. Угловой размер Земли с расстояния 1,5 млн км — 29,3′, а Солнца с 1 а. е. + 1,5 млн км — 31,6′

1. Lagrange, Joseph-Louis. Tome 6, Chapitre II: Essai sur le problème des trois corps // Oeuvres de Lagrange : . — Gauthier-Villars, 1867–92. — P. 229–334.
2. 1 2 Расчёт положения точек Лагранжа
3. Расчёт положения точек L4 и L5 (другой вариант)
4. ISEE-3/ICE profile by NASA Solar System Exploration
5. NSSDC Master Catalog: ISEE 3 / ICE
6. http://www.srl.caltech.edu/ACE/ASC/DATA/ace_dly_reprts/HTML/December_text_1997.html
7. Nation’s first operational satellite in deep space reaches final orbit, NOAA (June 8, 2015). Дата обращения 8 июня 2015.
8. LISA Pathfinder Will Concludee Trailblazing Mission. ESA Science and Technology. ESA (20 June 2017).
9. http://esamultimedia.esa.int/docs/edu/HerschelPlanck/EN_13e_L_Points_EarthMoonSystem.pdf
10. Ken Murphy. EML-1: the next logical destination (англ.). The Space Review (January 24, 2011). Дата обращения 5 ноября 2017.
11. Zegler, Frank; Bernard Kutter. Evolving to a Depot-Based Space Transportation Architecture. AIAA SPACE 2010 Conference & Exposition. AIAA (2 сентября 2010). — «L2 is in deep space far away from any planetary surface and hence the thermal, micrometeoroid, and atomic oxygen environments are vastly suberior to those in LEO. Thermodynamic stasis and extended hardware life are far easier to obtain without these punishing conditions seen in LEO. L2 is not just a great gateway – it is a great place to store propellants. … L2 is an ideal location to store propellants and cargos: it is close, high energy, and cold. More importantly, it allows the continuous onward movement of propellants from LEO depots thus subpressing their size and effectively minimizing the near-earth boiloff penalties». Дата обращения 25 января 2011. Архивировано 24 августа 2011 года.
12. 1 2 The Lagrange points // Australian Space Academy. — Дата обращения: 07.11.2017.
13. Could There Be a Planet Hidden on the Opposite Side of our Sun? PopSci asks the scientist who has peered around it (англ.)
14. Новости миссии STEREO на сайте НАСА
15. Tantardini, Marco; Fantino, Elena; Yuan Ren, Pierpaolo Pergola, Gerard Gymez and Josep J. Masdemont (2010). “Spacecraft trajectories to the L3 point of the Sun–Earth three-body problem”. Celestial Mechanics and Dynamical Astronomy (Springer). Используется устаревший параметр |coauthors= (справка)
16. Астрономы обнаружили у Земли первый троянский спутник
17. List of Jupiter Trojans
18. List Of Neptune Trojans. Minor Planet Center. Дата обращения 27 октября 2010. Архивировано 24 августа 2011 года.
19. Belbruno, E.; J. Richard Gott III (2005). «Where Did The Moon Come From?». The Astronomical Journal 129 (3): 1724—1745. arXiv: astro-ph/0405372
20. Впервые найдены две планеты на одной орбите
21. Beatty, Kelly. Kepler Finds Planets in Tight Dance. Sky and Telescope (2011). Дата обращения 11 марта 2011. Архивировано 25 января 2013 года.
22. Астронет > Тесные двойные звезды на поздних стадиях эволюции
23. 1 2 WMAP Observatory — Lagrange points (NASA)
24. Genesis: Search for Origins | Mission | JPL | NASA. genesismission.jpl.nasa.gov. Дата обращения 26 марта 2019.
25. Lenta.ru о телескопе «Гершель»
26. Космический телескоп «Планк» стал самым холодным объектом во Вселенной. Lenta.ru (6 июля 2009). Дата обращения 14 августа 2010. Архивировано 24 августа 2011 года.
27. The James Webb Space Telescope (NASA) (англ.)
28. Российско-немецкую обсерваторию «Спектр-РГ» запустят лишь в 2017 году, РИА Новости (22 апреля 2013).
29. Запуск российской космической обсерватории «Спектр-РГ» перенесен на 2019 год, Коммерсантъ (19 апреля 2018).
30. Европейское космическое агентство в 2024 году запустит телескоп PLATO
31. Space.com: The Search for the Solar System’s Lost Planet (англ.)
32. Александр Сергеев. «Лестница Лагранжа» (врезка к статье Игоря Афанасьева и Дмитрия Воронцова «Межпланетная эквилибристика»), «Вокруг света», № 8 (2815) 2008.
33. Queqiao relay satellite launched ahead of Chang’e-4 lunar mission (20 май 2018).
34. Китайский спутник-ретранслятор добрался до «рабочего места» за обратной стороной Луны, nplus1 (14 Июнь 2018). Дата обращения 23 октября 2018.

Ссылки

• Точки Лагранжа (англ.)
• Точки Лагранжа в научной фантастике

Типы Основные Геоцентрические Вокруг других небесных тел и точек
i {\displaystyle i\,\!} Наклонение Ω {\displaystyle \Omega \,\!} Долгота восходящего узла e {\displaystyle e\,\!} Эксцентриситет ω {\displaystyle \omega \,\!} Аргумент перицентра a {\displaystyle a\,\!} Большая полуось M o {\displaystyle M_{o}\,\!} Средняя аномалия на эпоху ν {\displaystyle \nu \,\!} Истинная аномалия b {\displaystyle b\,\!} Малая полуось E {\displaystyle E\,\!} Эксцентрическая аномалия L {\displaystyle L\,\!} Средняя долгота l {\displaystyle l\,\!} Истинная долгота T {\displaystyle T\,\!} Период обращения Параметры Классические Другие
	Другие темы астродинамики

Что это за «точки», чем они привлекательны в космических проектах и есть ли практика их использования? С этими вопросами редколлегия портала «Планета Королева» обратилась к доктору технических наук Юрию Петровичу Улыбышеву.

Проводит интервью Волков Олег Николаевич, заместитель руководителя проекта «Великое начало».

Волков О.Н.: В гостях интернет портала «Планета Королева заместитель руководителя научно-технического центра ракетно-космической корпорации «Энергия», начальник отдела космической баллистики, доктор технических наук Юрий Петрович Улыбышев. Юрий Петрович, добрый день!

Улыбышев Ю.П..: Добрый день.

В.: Существование на околоземной орбите пилотируемых комплексов это не диковинка. Это обычное, привычное дело. В последнее время в международном космическом сообществе проявляется интерес к другим космическим проектам, в которых предполагается размещать космические комплексы, в том числе, и пилотируемые в, так называемых, точках Лагранжа. Среди них проект посещаемых космических станций, проект станций, размещаемых для поиска опасных астероидов и слежения Луны.

Что такое точки Лагранжа? В чем их существо с точки зрения небесной механики? Какова история теоретических исследований по данному вопросу? Каковы основные результаты исследований?

У.: В нашей солнечной системе имеется большое количество природных эффектов, связанных с движением Земли, Луны, планет. К ним относятся и, так называемые, точки Лагранжа. В научной литературе их чаще даже называют точками либрации. Чтобы объяснить физическую суть этого явления, для начала рассмотрим простую систему. Есть Земля, и вокруг нее по круговой орбите летает Луна. Ничего больше в природе нет. Это, так называемая, ограниченная задача трех тел. И вот в этой задаче мы рассмотрим космический аппарат и его возможное движение.

Самое первое, что приходит на ум рассмотреть: а что будет, если космический аппарат находится на линии, соединяющей Землю и Луну. Если мы будем двигаться по этой линии, то у нас есть два гравитационных ускорения: притяжение Земли, притяжение Луны, и плюс есть центростремительное ускорение за счет того, что эта линия постоянно вращается. Очевидно, что в какой-то точке все эти три ускорения вследствие того, что они разнонаправлены и лежат на одной линии, могут обнулиться, т.е. это будет точка равновесия. Вот такую точку и называют точкой Лагранжа, либо либрационной точкой. На самом деле таких точек пять: три из них находятся на вращающейся линии, соединяющей Землю и Луну, их называют коллинеарными точками либрации. Первая, которую мы с вами разобрали, обозначают L1, вторая находится за Луной — L2, и третья коллинеарная точка — L3 находится с обратной стороны Земли по отношению к Луне. Т.е. на этой линии, но в противоположном направлении. Это первые три точки.

Есть еще две точки, которые находятся с двух сторон вне этой линии. Их называют треугольными точками либрации. Все эти точки показаны на этом рисунке (Рис.1). Вот такая идеализированная картинка.

Рис.1. Точки либрации системы Земля – Луна

Теперь, если мы поместим в любую из этих точек космический аппарат, то в рамках вот такой простой системы он всегда там и останется. Если мы чуть – чуть отклонимся от этих точек, то в их окрестности могут существовать периодические орбиты, их называют еще гало-орбитами (см. Рис.2), и космический аппарат сможет двигаться вокруг этой точки по вот таким своеобразным орбитам. Если говорить о точках либрации L1, L2 системы Земля – Луна, то период движения по этим орбитам будет порядка 12 — 14 суток, и они могу быть выбраны совершенно разным образом.

Рис.2. Гало-орбиты системы Земля — Луна

На самом деле, если мы вернемся к реальной жизни и рассмотрим вот эту задачу уже в точной постановке, то все окажется гораздо сложнее. Т.е. космический аппарат не может находиться очень долго, больше, скажем, одного периода, в движении по такой вот орбите, не может оставаться на ней, за счет того, что:

— во-первых, орбита Луны вокруг Земли не является круговой – она имеет небольшую эллиптичность;

— кроме того, на космический аппарат будет действовать притяжение Солнца, давление солнечного света.

В итоге космический аппарат не сможет оставаться на такой орбите. Поэтому, с точки зрения реализации космического полета по подобным орбитам, необходимо выведение космического аппарата на соответствующую гало-орбиту и затем периодическое проведение маневров по ее поддержанию.

По меркам межпланетных полетов затраты топлива на поддержание для таких орбит достаточно малы, не больше 50 – 80 м/сек в год. Для сравнения могу сказать, поддержание орбиты геостационарного спутника в год это тоже 50 м/сек. Там мы удерживаем геостационарный спутник около неподвижной точки — эта задача гораздо проще. Здесь мы должны удерживать космический аппарат в окрестности вот такой гало-орбиты. В принципе, практически эта задача реализуема. Более того, она реализуема с использованием двигателей малой тяги, и каждый маневр это доля метра или единицы м/сек. Отсюда напрашивается возможность использования орбит в окрестности этих точек для космических полетов, в том числе, пилотируемых.

Теперь, с точки зрения, а почему они выгодны, и чем они интересны, именно, для практической космонавтики?

Если вы все помните, американский проект «APOLLO», в котором использовалась окололунная орбита, с которой спускался аппарат, приземлялся на поверхность Луны, через некоторое время возвращался на окололунную орбиту и затем летел к Земле. Окололунные орбиты представляют определенный интерес, но они не всегда удобны для пилотируемой космонавтики. У нас могут быть различные нештатные ситуации, кроме того естественно желание изучать Луну не только в окрестности какого-то района, а вообще изучать всю Луну. В итоге оказывается, что использование окололунных орбит связано с рядом ограничений. Ограничения накладываются на даты старта, на даты возврата с окололунной орбиты. Параметры окололунных орбит могут зависеть от располагаемой энергетики. Скажем, полярные районы могут быть недоступны. Но самый главный, наверное, аргумент в пользу космических станций в окрестностях точек либрации заключается в том, что:

— первое, мы можем стартовать с Земли в любой момент времени;

— если станция находится в точке либрации, и космонавты должны лететь на Луну, они могут из точки либрации, вернее с гало-орбиты, лететь в любую точку на поверхности Луны;

— теперь, когда экипаж прилетел: с точки зрения пилотируемой космонавтики, очень важно обеспечение возможности быстрого возврата экипажа в случае каких-то нештатных ситуаций, болезней членов экипажа и т.п. Если мы говорим про окололунную орбиту, нам может понадобиться ожидание, допустим, времени старта 2 недели, а здесь мы можем стартовать в любой момент времени – с Луны до станции в точку либрации и затем к Земле, либо, в принципе, сразу к Земле. Такие преимущества достаточно явным образом видны.

Имеются варианты использования: L1 или L2. Есть определенные различия. Как вы знаете, Луна повернута к нам всегда одной и той же стороной, т.е. период ее собственного вращения равен периоду ее движения вокруг Земли. В итоге, обратная сторона Луны никогда не видна с Земли. В этом случае можно выбрать гало-орбиту такую, что она всегда будет находиться на линии видимости с Землей и иметь возможность осуществления связи, наблюдений и еще каких-то экспериментов, связанных с обратной стороной Луны. Таким образом, космические станции, размещенные в точке либо в точке L1, либо в точке L2, для пилотируемой космонавтики могут иметь определенные преимущества. Кроме того, интересным является то, что между гало-орбитами точек L1 или L2 можно осуществить, так называемый, низкоэнергетический перелет, буквально, 10 м/сек, и мы перелетим с одной гало-орбиты на другую.

В.: Юрий Петрович, у меня вопрос: точка L1 находится на линии между Луной и Землей, и, как я понимаю, с точки зрения обеспечения связи между космической станцией и Землей, более удобна. Вы говорили, что L2, точка, которая находится за Луной, тоже представляет интерес для практической космонавтики. А как обеспечить связь с Землей, если станция будет находиться в точке L2?

У.: Любая станция, находясь на орбите в окрестностях точки L1, имеет возможность непрерывной связи с Землей, любая гало-орбита. Для точки L2 несколько сложнее. Это связано с тем, что космическая станция при движении по гало-орбите может оказаться по отношению к Земле, как бы, в тени Луны, и связь тогда невозможна. Но можно построить такую гало-орбиту, которая всегда будет иметь возможность связи с Землей. Это специально выбранная орбита.

В.: Это несложно сделать?

У.: Да, можно сделать, и, так как ничто не удается сделать бесплатно, потребуется несколько большего расхода топлива. Скажем, вместо 50 м/сек будет 100 м/сек. Наверное, это не самый критичный вопрос.

В.: Еще один уточняющий вопрос. Вы говорили, что энергетически легко перелететь из точки L1 в точку L2, и обратно. Правильно я понимаю, что не имеет смысла создавать две станции в районе Луны, а достаточно иметь одну станцию, которая энергетически легко переходит в другую точку?

У.: Да, кстати говоря, наши партнеры по международной космической станции предлагают один из вариантов для обсуждения развития проекта МКС в виде космической станции с возможностью перелета от точки L1 в точку L2, и обратно. Это вполне реализуемо и обозримо по времени перелета (скажем, 2 недели) и может быть использовано для пилотируемой космонавтики.

Еще я хотел сказать, что на практике полеты по гало-орбитам в настоящее время были реализованы американцами по проекту ARTEMIS. Это примерно 2-3 года назад. Там два космических аппарата летали в окрестностях точек L1 и L2 с поддержанием соответствующих орбит. Один аппарат совершил перелет из точки L2 в точку L1. Вся эта технология на практике реализована. Конечно, хотелось, чтобы это сделали мы.

В.: Ну, у нас еще все впереди. Юрий Петрович, следующий вопрос. Как я понял из Ваших рассуждений, любая космическая система, состоящая из двух планет, имеет точки Лагранжа, или точки либрации. Существуют такие точки для системы Солнце – Земля, и в чем привлекательность этих точек?

У.: Да, конечно, совершенно правильно. В системе Земля – Солнце имеются тоже точки либрации. Их тоже пять. В отличие от окололунных точек либрации полет в тех точках может быть привлекателен уже для совсем других задач. Если говорить конкретно, то наибольший интерес представляют точки L1 и L2. Т.е. точка L1 по направлению от Земли к Солнцу, а точка L2 в противоположном направлении на линии, соединяющей Землю и Солнце.

Так вот, первый полет в точку L1 в системе Солнце — Земля был осуществлен в 1978 году. С тех пор было реализовано несколько космических миссий. Основной лейтмотив таких проектов был связан с наблюдением за Солнцем: за солнечным ветром, за солнечной активностью, в том числе. Есть системы, которые используют предупреждение о каких-то активных процессах на Солнце, влияющих на Землю: на наш климат, на самочувствие людей и т.д. Это то, что касается точки L1. Она в первую очередь интересна человечеству возможностью наблюдения за Солнцем, за его активностью и за процессами, которые проходят на Солнце.

Теперь точка L2. Точка L2 тоже интересна и, в первую очередь, для астрофизики. И связано это с тем, что космический аппарат, размещенный в окрестностях этой точки, может использовать, например, радиотелескоп, который будет экранирован от излучения со стороны Солнца. Он будет направлен противоположно от Земли и Солнца и может позволить проводить более чисто астрофизические наблюдения. Они не зашумлены Солнцем, ни какими-то отраженными излучениями со стороны Земли. И еще интересно, т.к. мы движемся вокруг Солнца, за 365 дней делаем полный оборот, то подобным радиотелескопом можно рассмотреть любое направление вселенной. Такие проекты тоже есть. Вот сейчас у нас в Физическом институте Российской Академии Наук разрабатывается такой проект «Миллиметрон». В этой точке тоже ряд миссий был реализован, и космические аппараты летают.

В.: Юрий Петрович, с точки зрения поиска опасных астероидов, которые могут угрожать Земле, в какой точке надо размещать космические аппараты, чтобы они следили за опасными астероидами?

У.: Вообще-то, такого прямого, очевидного ответа на этот вопрос, мне кажется, нет. Почему? Потому что движущиеся астероиды по отношению к солнечной системе, как бы, группируются в ряд семейств, у них совершенно разные орбиты и, по моему мнению, можно в окололунной точке поместить аппарат для одного типа астероидов. То, что касается точек либрации системы Солнце — Земля, также можно посмотреть. Но такого очевидного, прямого ответа: «такая-то точка в такой-то системе» — мне кажется, трудно дать. Но, в принципе, точки либрации могут быть привлекательны для защиты Земли.

В.: Правильно я понимаю, солнечная система имеет еще много интересных мест, не только Земля – Луна, Земля – Солнце. А какие еще интересные места солнечной системы можно использовать в космических проектах?

У.: Дело в том, что в солнечной системе в том виде, в каком она существует, помимо эффекта, связанного с точками либрации, существует еще ряд таких эффектов, связанный с взаимным движением тел в солнечной системе: и Земли, и планет, и т.д. У нас в России я, к сожалению, не знаю работ на эту тему, а вот, в первую очередь, американцы и европейцы выявили, что в солнечной системе существуют, так называемые, низкоэнергетические перелеты (причем, эти исследования — достаточно сложные и в математическом плане работы, и в плане вычислительном – они требуют больших вычислительных суперкомпьютеров).

Вот, к примеру, возвращаемся к точке L1 системы Земля — Луна. По отношению к этой точке можно построить (это привлекательно для автоматических аппаратов) перелеты по всей солнечной системе, давая небольшие, по меркам межпланетных полетов, импульсы порядка нескольких сотен м/сек. И тогда этот космический аппарат начнет медленное движение. При этом можно построить траекторию таким образом, что она обойдет ряд планет.

В отличие от прямых межпланетных перелетов это будет длительный процесс. Поэтому, для пилотируемой космонавтики он не очень подходит. А для автоматических аппаратов он очень может быть очень привлекательным.

Вот на картинке (Рис.3) показана иллюстрация этих перелетов. Траектории, как бы, зацепляются друг за друга. Переход с гало-орбиты с L1 в L2. Он стоит достаточно немного. Вот там — то же самое. Мы как бы скользим по этому тоннелю, и в месте зацепления или близком к зацеплению с другим тоннелем мы даем небольшой маневр и перелетаем, идем к другой планете. Вообще, очень интересное направление. Оно называется «Superhighway» (по крайней мере, американцы используют такой термин).

Рис.3. Солнечная система пронизана туннелями переходов с минимальной энергетикой
(рисунок из зарубежных публикаций)

Практическая реализация частично была сделана американцами в рамках проекта GENESIS. Сейчас они тоже в этом направлении работают. Мне кажется, это одно из наиболее перспективных таких направлений в развитии космонавтики. Потому что все-таки с теми двигателями, «движителями», которые у нас имеются в настоящее время, я имею в виду двигатели большой тяги и двигатели электрореактивные (которые пока имеют очень маленькую тягу и требуют большую энергию), мы сдвинуться в плане освоения солнечной системы или дальнейшего изучения сильно не можем. А вот такие многолетние или даже десятилетние задачи перелета могут быть для исследований очень интересны. Так же, как Вояджер. Он летал, кажется, с 1978 года или 1982 (с 1977 года – ред.), сейчас ушел за пределы солнечной системы. Это направление очень сложно. Во-первых, сложно в математическом плане. Кроме того, здесь анализ и расчеты по механике перелетов требуют высоких ресурсов компьютеров, т.е. на персональном компьютере это сомнительно обсчитать, нужно использовать суперкомпьютеры.

В.: Юрий Петрович, можно систему низкоэнергетичных переходов использовать для организации космического солнечного патруля – постоянной системы мониторинга солнечной системы с имеющимися ограничениями по топливу, которые у нас есть?

У.: Даже между Землей и Луной, а также, допустим, между Землей и Марсом, Землей и Венерой существуют, так называемые квазипериодические траектории. Подобно тому, как мы разбирали гало-орбиту, которая в идеальной задаче без возмущения существует, но, когда мы накладываем реальные возмущения, мы вынуждены корректировать каким-то образом орбиту. Эти квазипериодические орбиты требуют тоже небольших, по меркам межпланетных полетов, когда характеристические скорости – это сотни м/сек. С точки зрения космического патруля для наблюдения за астероидами они могут быть привлекательны. Единственный минус в том, что они слабо подходят для нынешней пилотируемой космонавтики из-за большой длительности перелетов. А с точки зрения энергии, и даже с теми двигателями, которые сейчас в нашем столетии есть, можно сделать достаточно интересные проекты.

В.: Правильно я понимаю, точки либрации системы Земля — Луна, Вы предполагаете для пилотируемых объектов, а точки, о которых Вы говорили раньше, для автоматов?

У.: Еще я хотел бы добавить один момент, космическая станция в L1 или в L2 может служить для запуска небольших космических аппаратов (американцы называют такой подход «Gate Way» — «Мост во вселенную»). Аппарат может с использованием низкоэнергетических перелетов как-то периодически двигаться вокруг Земли на очень больших расстояниях, либо осуществлять перелет к другим планетам или даже облет нескольких планет.

В.: Если немного пофантазировать, то в дальнейшем Луна будет являться источником космического топлива, и на точку либрации системы Земля — Луна будет поступать лунное топливо, то можно заправлять космические аппараты космическим топливом и посылать космические патрули по всей солнечной системе.

Юрий Петрович, Вы рассказывали об интересных явлениях. Их исследовали американская сторона (NASA), а в нашей стране занимаются этими проектами?

У.: Проектами, связанными с точками либрации системы Земля – Луна, насколько я знаю, наверное, не занимаются. Вот проектами, связанными с точками либрации системы Солнце – Земля, занимаются. У нас большой опыт в этом направлении имеют Институт прикладной математики Российской Академии Наук имени Келдыша, Институт космических исследований, некоторые ВУЗы в России пытаются заниматься подобными проблемами. Но такого систематического подхода, большой программы, потому что программа должна начинаться с подготовки кадров, причем кадров с очень высокой квалификацией, нет. В традиционных курсах по космической баллистике, по небесной механике сама механика движения космических аппаратов в окрестности точек либрации, низкоэнергетические перелеты, практически отсутствует.

Я должен отметить, во времена Советского Союза подобными программами занимались более – менее активно, и специалисты были, как я уже упоминал, в Институте прикладной математики, ИКИ, ФИАН. Сейчас многие из них находится в таком возрасте… А большое количестве молодежи, которая занималась бы этими проблемами, проглядывается весьма слабо.

Я упомянул американцев не в том плане, чтобы их похвалить. Дело в том, что в США этими проблемами занимаются очень крупные подразделения. В первую очередь, в лаборатории JPL NASA большой коллектив работает, и они осуществили, наверное, большинство американских проектов межпланетной космонавтики. Во многих американских университетах, в других центрах, в NASA, работает большое количество специалистов с хорошей подготовкой, с хорошим компьютерным оснащением. Они идут по этой проблеме, в этом направлении очень широким фронтом.

У нас, к сожалению, это как-то скомкано. Если бы такая программа в России и появилась бы, представляла в целом большой интерес, то на развертывание этих работ, могло бы уйти достаточно длительное время, начиная с подготовки кадров и кончая исследованиями, расчетами, разработкой соответствующих космических аппаратов.

В.: Юрий Петрович, а какие ВУЗы готовят специалистов по небесной механике в нашей стране?

У.: Насколько я знаю, в МГУ, в Петербургском университете есть кафедра небесной механики. Там такие специалисты есть. Сколько их, я затрудняюсь ответить.

В.: Потому что, чтобы начать реализовывать практическую сторону вопроса, надо сначала стать глубоким специалистом, а для этого надо иметь соответствующую специальность.

У.: И иметь очень хорошую математическую подготовку.

В.: Хорошо. А можете сейчас привести список литературы, который помог бы тем людям, которые не имеют сейчас специальной математической подготовки?

У.: На русском языке, насколько я знаю, посвященная точкам либрации, есть одна монография Маркеева. Если память мне не изменяет, она называется так «Точки либрации в небесной механике и космодинамике». Она, примерно, в 1978 году выходила. Есть справочник под редакцией Дубошина «Справочник по небесной механике и астродинамике». Он выдержал 2 издания. Насколько я помню, в нем тоже такие вопросы есть. Остальное можно почерпнуть, во-первых, на сайте Института прикладной математики есть электронная библиотека и свои препринты (отдельно изданные статьи) по этому направлению. Они печатают в свободном доступе в Интернете. С помощью поисковой системы можно найти соответствующие препринты и их посмотреть. Очень много доступного с Интернете материала на английском языке.

В.: Спасибо за увлекательный рассказ. Я надеюсь, эта тема будет интересна для наших пользователей интернет ресурса. Спасибо Вам огромное!

Интервью доктора технических н…

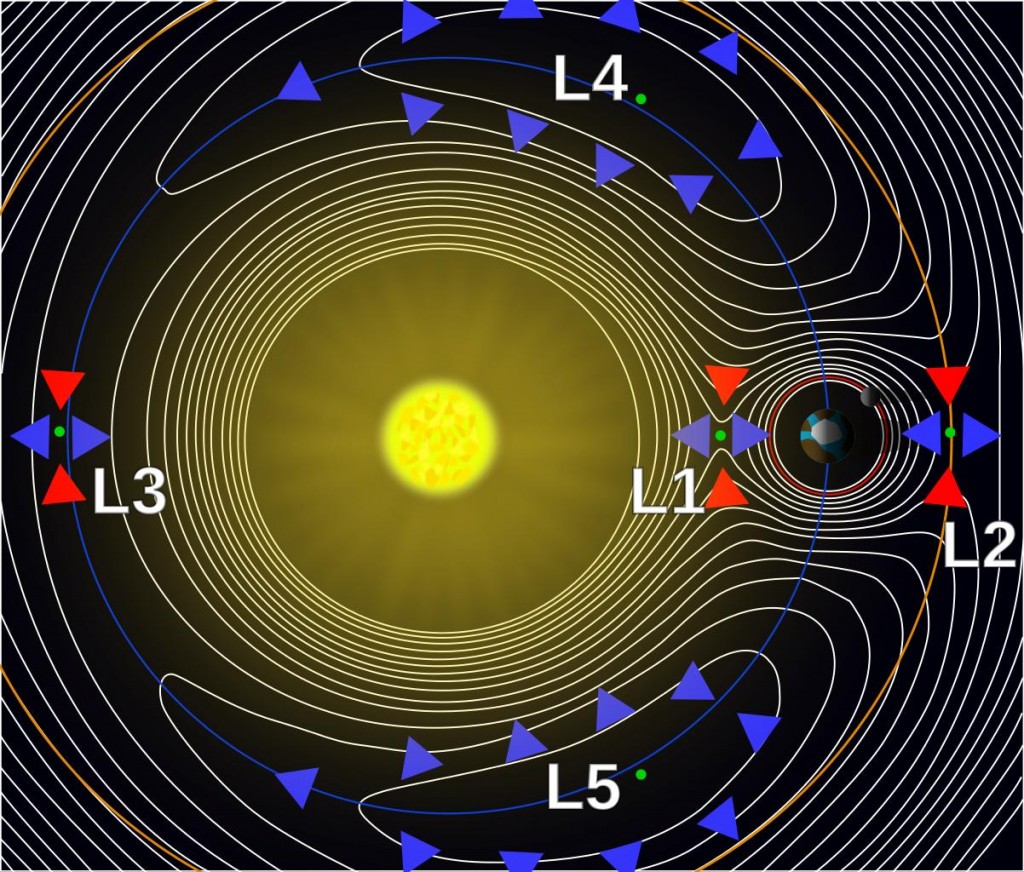
Точки Лагранжа и эквипотенциальные поверхности системы двух тел

Точки Лагранжа – это области в системе двух космических тел с большой массой, в которых третье тело с небольшой массой, может быть неподвижным на протяжении долгого периода времени относительно этих тел.

Общие сведения

В астрономической науке точки Лагранжа называют еще точками либрации (либрация от лат. librātiō – раскачивание) или L-точками. Впервые они были обнаружены в 1772 году известным французским математиком Жозефом Луи Лагранжем.

Точки Лагранжа наиболее часто упоминаются при решении ограниченной задачи трех тел. В этой задаче три тела имеют круговые орбиты, но масса одного из них меньше массы любого из двух других объектов. Два крупных тела в этой системе обращаются вокруг общего центра масс, имея постоянную угловую скорость. В области вокруг этих тел находится пять точек, в которых тело, масса которого меньше массы любого из двух крупных объектов, может оставаться неподвижным. Это происходит за счет того, что силы гравитации, которые действуют на это тело, компенсируются центробежными силами. Эти пять точек и называются точками Лагранжа.

Точки Лагранжа лежат в плоскости орбит массивных тел. В современной астрономии они обозначаются латинской буквой «L». Также в зависимости от своего места расположения каждая из пяти точек имеет свой порядковый номер, который обозначается числовым индексом от 1 до 5. Первый три точки Лагранжа называют коллинеарными, остальные две – троянскими или треугольными.

Расположение ближайших точек Лагранжа и примеры точек

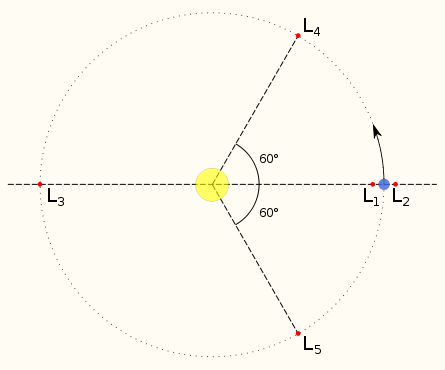
Диаграмма, показывающая положения точек Лагранжа

В независимости от типа массивных небесных тел, точки Лагранжа всегда будут иметь одинаковое местоположение в пространстве между ними. Первая точка Лагранжа находится между двумя массивными объектами, ближе к тому, который имеет меньшую массу. Вторая точка Лагранжа находится за менее массивным телом. Третья точка Лагранжа находится на значительном расстоянии за телом, обладающим большей массой. Точное место расположения этих трех точек рассчитывается при помощи специальных математических формул индивидуально для каждой космической двойной системы, учитывая ее физические характеристики.

Если говорить о ближайших к нам точкам Лагранжа, то первая точка Лагранжа в системе Солнце-Земля будет находиться на расстоянии полтора миллиона километров от нашей планеты. В этой точке притяжение Солнца будет на два процента сильнее, чем на орбите нашей планеты, в то время как уменьшение необходимой центростремительной силы будет в два раза меньше. Оба этих эффекта в данной точке будут уравновешены гравитационным притяжением Земли.

Первая точка Лагранжа в системе Земля-Солнце является удобным наблюдательным пунктом за главной звездой нашей планетарной системы – Солнцем. Именно здесь ученые-астрономы стремятся разместить космические обсерватории для наблюдения за этой звездой. Так, к примеру, в 1978 году вблизи этой точки расположился космический аппарат ISEE-3, предназначенный для наблюдения за Солнцем. В последующие годы в район этой точки были запущены космические аппараты SOHO, DSCOVR, WIND и ACE.

Вторая и третья точки Лагранжа

Гайя, телескоп, расположившийся во второй точке Лагранжа

Вторая точка Лагранжа находится в двойной системе массивных объектов за телом, обладающим меньшей массой. Применение этой точки в современной астрономической науке сводится к размещению в ее районе космических обсерваторий и телескопов. В данный момент в этой точке находятся такие космические аппараты, как «Гершель», «Планк», WMAP и Gaia. В 2018 году туда должен отправиться еще один космический аппарат – «Джемс Уэбб».

Третья точка Лагранжа находится в двойной системе на значительном расстоянии за более массивным объектом. Если говорить о системе Солнце-Земля, то такая точка будет находиться за Солнцем, на расстоянии чуть большем, чем то, на котором находится орбита нашей планеты. Связано это с тем, что, несмотря на свои малые размеры, Земля все же оказывает незначительное гравитационное влияние на Солнце. Спутники, размещенные в этой области космоса, могут передавать на Землю точную информацию о Солнце, появлении новых «пятен» на звезде, а также передавать данные о космической погоде.

Четвертая и пятая точки Лагранжа

Троянские астероиды Юпитера в представлении художника

Четвертая и пятая точки Лагранжа называются треугольными. Если в системе, состоящей из двух массивных космических объектов, вращающихся вокруг общего центра масс, на основе линии, соединяющей эти объекты, мысленно начертить два равносторонних треугольника, вершины которого будут соответствовать положению двух массивных тел, то четвертая и пятая точки Лагранжа будут находиться в месте третьих вершин данных треугольников. То есть, они будут находиться в плоскости орбиты второго массивного объекта в 60 градусах сзади и впереди него.

Треугольные точки Лагранжа также называют еще и «троянскими». Второе название точек происходит от троянских астероидов Юпитера, которые являются ярчайшим наглядным проявлением четвертой и пятой точек Лагранжа в нашей Солнечной системе.

В данный момент четвертая и пятая точки Лагранжа в двойной системе Солнце-Земля никак не используются. В 2010 году в четвертой точке Лагранжа этой системы ученые обнаружили достаточно крупный астероид. В пятой точке Лагранжа на данном этапе никаких крупных космических объектов не наблюдается, однако последние данные говорят нам о том, что там находится большое скопление межпланетной пыли.

Интересные факты

1. В 2009 году два космических аппарата STEREO пролетели через четвертую и пятую точки Лагранжа.
2. Точки Лагранжа часто используются в научно-фантастических произведениях. Часто в этих областях пространства, вокруг двойных систем, писатели-фантасты помещают свои вымышленные космические станции, мусорные свалки, астероиды и даже другие планеты.
3. В 2018 году во второй точке Лагранжа в двойной системе Солнце-Земля ученые планируют поместить космический телескоп «Джеймс Уэбб». Этот телескоп должен заменить действующий космический телескоп «Хаббл», который находится в этой точке. В 2024 году ученые планируют поместить в этой точке еще один телескоп «PLATO».
4. Первая точка Лагранжа в системе Луна-Земля могла бы стать отличным местом для размещения пилотируемой орбитальной станции, которая могла бы значительно уменьшить затрату ресурсов, необходимых для того, чтобы добраться с Земли на Луну.
5. Два космических телескопа «Планк» и «Гершель», которые были запущены в космос в 2009 году, в данный момент находятся во второй точке Лагранжа в системе Солнце-Земля.

Космические аппараты в точках Лагранжа системы Земля-Луна

Проводились ли эксперименты по размещению космических аппаратов в точках Лагранжа системы Земля-Луна?
Несмотря на то, что о так называемых точках либрации, существующих в космосе, и об их удивительных свойствах человечеству известно достаточно давно, использовать их в практических целях начали лишь на 22-й год космической эры. Но вначале вкратце расскажем о самих чудо-точках.
Впервые теоретически они были обнаружены Лагранжем (чье имя теперь и носят), как следствие решения так называемой задачи трех тел. Ученому удалось определить, где в пространстве могут находиться точки, в которых равнодействующая всех внешних сил обращается в ноль.
Точки делятся на устойчивые и неустойчивые. Устойчивые принято обозначать L4 и L5. Они располагаются в одной плоскости с основными двумя небесными телами (в данном случае — Землей и Луной), образуя с ними два равносторонних треугольника, за что их часто еще называют треугольными. В треугольных точках космический аппарат может находиться сколь угодно долго. Если же даже он отклонится в сторону, действующие силы все равно вернут его к положению равновесия. Космический аппарат словно попадает в гравитационную воронку, как бильярдный шар в лузу.
Однако, как мы сказали, существуют еще и неустойчивые точки либрации. В них космический аппарат, наоборот, находится словно на горе, являясь устойчивым лишь на самой ее вершине. Любое внешнее воздействие отклоняет его в сторону. Выйти в неустойчивую точку Лагранжа чрезвычайно сложно — для этого требуется сверхточная навигация. Поэтому аппарату приходится двигаться лишь вблизи самой точки по так называемой «гало-орбите», время от времени расходуя для ее поддержания топливо, правда, совсем немного.
В системе Земля-Луна неустойчивых точек три. Часто их еще называют прямолинейными, так как они расположены на одной линии. Одна из них (L1) находится между Землей и Луной, в 58 тыс. км от последней. Вторая (L2) — расположена так, что ее никогда не видно с Земли — она прячется за Луной в 65 тыс. км от нее. Последняя же точка (L3), наоборот, никогда не видна с Луны, так как ее загораживает Земля, от которой до нее примерно 380 тыс. км.
Хотя находиться в устойчивых точках и выгоднее (не требуется расходовать горючее), космические аппараты все же пока познакомились лишь с неустойчивыми, вернее, только с одной из них, да и то относящейся к системе Солнце-Земля. Она находится внутри этой системы, в 1.5 млн. км от нашей планеты и так же как точка между Землей и Луной имеет обозначение L1. При взгляде с Земли она проецируется прямо на Солнце и может служить идеальным пунктом для слежения за ним.
Этой возможностью впервые воспользовался американский аппарат ISEE-3, запущенный 12 августа 1978 года. С ноября 1978 по июнь 1982 года он находился на «гало-орбите» вокруг точки Li, изучая характеристики солнечного ветра. По окончания этого срока именно ему, но уже переименованному в ICE, довелось стать первым в истории исследователем кометы. Для этого аппарат покинул точку либрации и, совершив несколько гравитационных маневров у Луны, в 1985 году осуществил пролет вблизи кометы Джакобини-Циннера. На следующий год он же исследовал комету Галлея, правда, только на дальних подступах.
Следующим посетителем точки L1 системы Солнце-Земля стала европейская солнечная обсерватория SOHO, запущенная 2 декабря 1995 года и, к сожалению, недавно потерянная из-за ошибки управления. За время ее работы было получено не мало важной научной информации и сделано множество интересных открытий.
Наконец, последним на сегодняшний день аппаратом, выведенным в окрестности L1, стал американский аппарат АСЕ, предназначенный для изучения космических лучей и звездного ветра. Он стартовал с Земли 25 августа прошлого года и в настоящее время успешно проводит свои исследования.
А что же дальше? Существуют ли новые проекты, связанные с точками либрации? Безусловно, существуют. Так, в США принято предложение вице-президента А. Гора о новом запуске в направлении точки L1 системы Солнце-Земля научно-образовательного аппарата «Триана», уже прозванного «Камерой Гора».
В отличие от своих предшественников он будет следить не за Солнцем, а за Землей. Наша планета из этой точки видна всегда в полной фазе и поэтому очень удобна для наблюдений. Ожидается, что картинки, полученные «Камерой Гора», будут практически в реальном времени поступать в сеть Интернет, и к ним будет открыт доступ для всех желающих.
Существует и российский «либрационный» проект. Это аппарат «Реликт-2», предназначенный для сбора информации о реликтовом излучении. Если для этого проекта найдется финансирование, то его ждет точка либрации L2 в системе Земля-Луна, то есть та, что спрятана за Луной.

Точки либрации — 5 точек равновесия, существующие в системе из двух массивных тел, где тело с меньшей массой вращается вокруг тела с большей массой. Такими системами, к примеру, являются Солнце-Земля, Земля-Луна, Солнце-Юпитер, Марс-Фобос и так далее.

Если бы движение происходило по строго круговым орбитам, и тела не испытывали никакого внешнего воздействия, то в 5 точках притяжение двух тел уравновешивало бы друг друга, и космический аппарат, помещённый в любую из этих точек, оставался бы в состоянии покоя.

Расположение этих точек указано на рисунке выше. L1, L2 и L3 лежат на прямой, соединяющей тела, треугольные точки L4 и L5 расположены по бокам.

В реальности всё несколько сложнее: планеты вращаются не по круговым, а по эллиптическим орбитам; к тому же, они испытывают гравитационное возмущение от других небесных тел. Поэтому неподвижно зафиксировать космический аппарат в точках либрации не получится, необходимо постоянно поддерживать стабильность его орбиты. Однако поддерживать орбиту вокруг точки либрации не более затратно, чем орбиту вокруг одной из планет. В связи с этим эти точки вызывают интерес у проектировщиков космических миссий.

Зачем они нужны?

Целесообразность вывода космического аппарата на орбиту вокруг точек либрации в случае разных систем разная. Рассмотрим основные, наиболее близкие нам варианты.

Солнце-Земля

Точка L1 в этой системе интересна для постоянного наблюдения за Солнцем. Точка L2, напротив, интересна для наблюдений, которым солнечное излучение только мешает. (ведь в L2 космический аппарат всё время находится в тени Земли)

С точкой L3 связаны легенды об «Антиземле» — планете-двойнике Земли, спрятанной от нас по ту сторону Солнца. Эта область уже фотографировалась космическими аппаратами, кроме залётных астероидов там, конечно же, ничего нет. Однако в будущем, когда мы наконец начнём активно летать по Солнечной системе, оборудовать станцию в L3 будет очень удобно.

Земля-Луна

В этой системе больше всего интересна точка L2, поскольку она находится над обратной стороной Луны. Как известно, около половины лунной поверхности мы никогда с Земли не видим. Когда начнётся активное исследование обратной стороны Луны, это может вызвать значительные трудности для установления постоянной радиосвязи. Для решения этой проблемы предполагается оборудовать в L2 систему ретрансляторов.

Точка L1 является идеальным местом для строительства пилотируемой орбитальной станции, которая могла бы использоваться в процессе освоения нашего спутника.

Существующие проекты

Точки либрации постепенно начинают осваиваться мировыми космическими агентствами. Действующих и планируемых миссий довольно много, перечислю некоторые из них.

1) LISA Pathfinder. После открытия гравитационных волн в обсерватории LIGO, ESA объявила о планах построить в 2034 году в космосе огромный интерферометр, который будет в разы чувствительнее земного аналога. LISA Pathfinder должна протестировать необходимые для этого технологии. Этот аппарат начал свою научную деятельность в марте этого года, располагается он в точке L1 Солнце-Земля.

2) В октябре 2018 к точке L2 системы Солнце-Земля планируется запустить телескоп Джеймс Уэбб — наследника и приемника стремительно устаревающего Хаббла.

3) В 2017 году Россия планирует запустить в эту точку обсерваторию Спектр-РГ. Задачей этого аппарата является обзор всего неба в рентгеновском и гамма-диапазоне с чувствительностью, в 40 раз превышающей чувствительность предыдущего обзора, сделанного спутником ROSAT в 90-е годы.

4) В 2013 году в эту точку (L2 Солнце-Земля) был запущен европейский аппарат Gaia, который занят составлением подробной звёздной карты.

5) SOHO — совместный проект NASA и ESA, запущенный в 1995 году в точку L1 Солнце-Земля. Его основной задачей является изучение Солнца, однако также благодаря ему было открыто 2000 околосолнечных комет. Снимки, сделанные этим аппаратом, доступны всем желающим в Интернете.