Активные фильтры на оу
Такой фильтр был изготовлен для мощного автомобильного сабвуфера. Представленная схема — активный фильтр низких частот, который срезает все ненужные полосы, оставляя только низкие. Затем сигнал усиливается и подается на вход сабвуферного усилителя. Именно благодаря такому НЧ фильтру головка играет на низких частотах, (в простонародье называют БАСС).

Схема активного сабвуфера
На плате помимо фильтра НЧ также присутствует сумматор, который предназначен для суммирования сигнала обеих каналов. На вход этого блока подается сигнал с двух каналов (стереофонический), поступая на сумматор, сигнал превращается в один единый, это дает возможность получить дополнительное усиление. После суммирования, сигнал фильтруется и срезаются частоты ниже 16Гц и выше 300Гц. Регулирующий фильтр срезает сигнал от 35Гц — 150Гц.
Таким образом, мы получаем низкочастотный сигнал с возможностью регулировки в указанных пределах. Также имеется фазовый регулятор, который дает возможность согласовать сабвуфер с акустикой автомобиля.

В ФНЧ схеме я применил только пленочные конденсаторы, говорят в усилителях они лучше керамики, но и с керамическими работает очень хорошо, разница не слишком большая.

Монтаж выполнен на печатной плате, которая была создана методом ЛУТ, травил раствором лимонной кислоты и перекиси водорода.

 ФНЧ.lay
ФНЧ.lay
Такой сабвуфер питается от двухполярного источника питания (+/-15Вольт), поскольку работает совместно с мощным усилителем по схеме Ланзара. Если для питания усилителя и блока фильтров (как в моем случае) у вас только один источник питания, то блоку ФНЧ необходим двухполярный стабилизатор напряжения.
Такой блок сумматора и фильтра низких частот может работать буквально с любыми усилителями мощности. Три регулятора, один из них предназначен для регулировки громкости, другой для среза низких частот, третий — регулятор плавной фазы (о чем было сказано выше).

В моем случае были куплены только микросхемы, все остальные пассивные компоненты были сняты из старых плат. Пленочные конденсаторы на входе ФНЧ были выпаяны от старого телевизора, одним словом затраты на такой блок минимальны, не более 3$, взамен можете гордится тем, что аналогичный блок фильтров используют в современных автоусилителях, цена которых порядка 400$.
Содержание
Активный фильтр
 Пример активного фильтра высоких частот. Операционный усилитель U1 используется в качестве повторителя напряжения.
Пример активного фильтра высоких частот. Операционный усилитель U1 используется в качестве повторителя напряжения.
Активный фильтр — один из видов аналоговых электронных фильтров, в котором присутствует один или несколько активных компонентов, к примеру, транзистор или операционный усилитель.
В активных фильтрах используется принцип отделения элементов фильтра от остальных электронных компонентов схемы. Часто бывает необходимо, чтобы они не оказывали влияния на работу фильтра. Применение усилителей в активных фильтрах позволяет увеличить наклон частотной характеристики в полосе подавления, что недостижимо при каскадном соединении пассивных RC-цепочек.
Существует несколько различных типов активных фильтров, некоторые из которых также имеют и пассивную форму:
- Фильтр высоких частот — ослабляет (обычно значительно) амплитуды гармонических составляющих сигнала выше частоты среза.
- Фильтр низких частот — ослабляет (обычно значительно) амплитуды гармонических составляющих сигнала ниже частоты среза.
- Полосовой фильтр — ослабляет (обычно значительно) амплитуды гармонических составляющих сигнала выше и ниже некоторой полосы.
- Режекторный фильтр — ослабляет (обычно значительно) амплитуды гармонических составляющих сигнала в определённой ограниченной полосе частот.
> См. также
- Пассивный фильтр
- Фильтр Линквица — Райли
- Фильтр Саллена — Кея
Общие сведения
Активными фильтрами называют электронные усилители, содержащие RC-цепи, с помощью которых усилителю придаются определенные избирательные свойства.
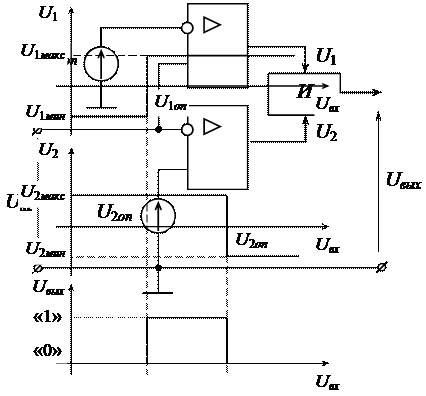
а
б
Рисунок 3.26 – Двухпороговый компаратор напряжения
Применение усилительных элементов выгодно отличает активные фильтры от фильтров на пассивных элементах.
К преимуществам активных фильтров в первую очередь следует отнести:
— способность усиливать сигнал, лежащий в полосе пропускания фильтра;
— возможность отказаться от применения таких нетехнологичных элементов, как катушки индуктивности, использование которых несовместимо с методами интегральной технологии;
— простота настройки;
— малые масса и объем, которые слабо зависят от полосы пропускания, что особенно важно при разработке устройств, работающих в низкочастотной области;
— простота каскадного включения при построении фильтров высоких порядков.
Вместе с тем активным фильтрам свойственны следующие недостатки, ограничивающие область их применения:
— невозможность использования в силовых цепях, например в качестве фильтров во вторичных источниках питания;
— необходимость использования дополнительного источника энергии, предназначенного для питания активных элементов усилителя;
— ограниченный частотный диапазон, определяемый собственными частотными свойствами используемых усилителей.
Несмотря на перечисленные недостатки, активные фильтры находят широкое практическое применение. Особый интерес представляют активные фильтры, выполненные на основе ОУ. Они позволяют получать стабильные и в тоже время недорогие частотно-избирательные цепи в диапазоне частот от 0 до 100 кГц. Применение активных фильтров на ОУ в области низких частот позволяет избавиться от громоздких конденсаторов и катушек индуктивности, которым, кроме всего прочего, присущи большие потери.
Основным параметром фильтра является его полоса пропускания – область частот, в пределах которой фильтр обладает малым ослаблением (затуханием). Как и в усилителях, она определяется по уровню уменьшения коэффициента усиления в 1,41 раза (на 3 дБ). Область частот, в пределах которой фильтр существенно ослабляет сигнал, называется полосой задержания (заграждения, подавления).
По характеру расположения полосы пропускания и полосы задержания активные фильтры, как и фильтры на пассивных элементах, подразделяются на:
— фильтры нижних частот (ФНЧ), пропускающие сигналы в диапазоне частот от w = 0 до w = wв (рисунок 3.27, а);
— фильтрыверхних частот (ФВЧ), пропускающие сигналы с частотой от w = wн до w ® ¥ (рисунок 3.27, б);
— полосовые фильтры (ПФ), пропускающие сигналы в диапазоне частот от wн до wв (рисунок 3.27, в);
— режекторные (заградительные) фильтры, не пропускающие сигналы в узком диапазоне частот от wзн до wзв (рисунок 3.27, г).
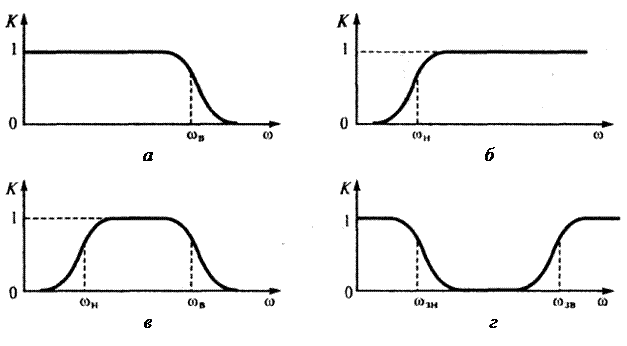
Рисунок 3.27 – АЧХ разных типов фильтров
Для решения конкретных задач по обработке сигналов в настоящее время разработано большое число различных схем активных фильтров. Наиболее известными из них являются фильтры Чебышева, Баттерворта и Бесселя. Основным различием этих фильтров является выбор математической функции для аппроксимации АЧХ фильтра.
Рассмотрим общие принципы применения ОУ с цепями частотно-зависимой ООС для формирования устройств с различными частотными свойствами.
Фильтры нижних и верхних частот
Простейшими активными фильтрами нижних и верхних частот первого порядка являются, соответственно, интегрирующий (рисунки 3.13, 3.14) и дифференцирующий (рисунки 3.16, 3.17) усилители. В них основным элементом, определяющим частотную характеристику усилителя, является конденсатор, включенный в цепь обратной связи.
Передаточные функции простейших фильтров представляют собой уравнения первого порядка, поэтому и фильтры называются фильтрами первого порядка. Наклон логарифмической АЧХ (ЛАЧХ) за пределами полосы пропускания у фильтров первого порядка составляет всего –20 дБ/дек, что свидетельствует о плохих избирательных свойствах таких фильтров.
Для улучшения избирательности нужно либо повышать порядок передаточной функции фильтра за счет введения дополнительных RC-цепей, либо последовательно включать несколько идентичных активных фильтров.
На практике наиболее часто в качестве фильтров используют ОУ с цепями ОС, работа которых описывается уравнениями второго порядка. При необходимости повысить избирательность системы несколько фильтров второго порядка включают последовательно (например, для получения ФНЧ четвертого порядка последовательно включают два ФНЧ второго порядка, для получения ФНЧ шестого порядка – три ФНЧ второго порядка и т. д.).
Активные фильтры низких и высоких частот второго порядка приведены на рисунке 3.28, а, б. У них, при соответствующем подборе номиналов резисторов и конденсаторов, спад ЛАЧХ за пределами полосы пропускания составляет 40 дБ/дек. Причем, как видно из рисунка 3.28, переход от фильтра нижних к фильтру верхних частот осуществляется заменой резисторов на конденсаторы, и наоборот.
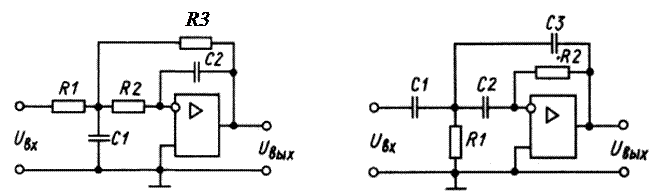
а б
Рисунок 3.28 – ФНЧ (а) и ФВЧ (б) второго порядка на операционном усилителе
Передаточная функция фильтра НЧ второго порядка описывается выражением
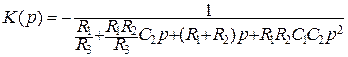 , (3.38)
, (3.38)
а фильтра ВЧ второго порядка – выражением
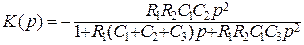 . (3.39)
. (3.39)
Частоты среза фильтров второго порядка соответственно равны:
— для ФНЧ
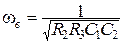 ; (3.40)
; (3.40)
— для ФВЧ
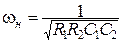 . (3.41)
. (3.41)
В последнее время широкое распространение получили активные ФНЧ и ФВЧ второго порядка, реализованные на повторителях напряжения (максимальное значение коэффициента усиления напряжения у таких фильтров в пределах полосы пропускания равно 1). Схемы названных фильтров показаны на рисунке 3.29, а (ФНЧ) и 3.29, б (ФВЧ).
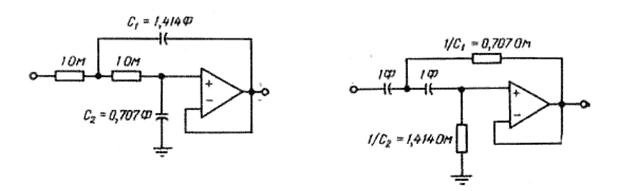
а б
Рисунок 3.29 – ФНЧ (а) и ФВЧ (б) второго порядка на повторителях напряжения
Последовательность расчета элементов фильтров, выполненных на основе повторителей, состоит в следующем:
а) по графикам (рисунок 3.30) выбрать подходящую характеристику фильтра (с учетом требуемой избирательности) и определить число полюсов, требующееся для получения желаемого затухания;
б) из схем на повторителях выбрать подходящую схему фильтра (рисунок 3.29);
в) пользуясь данными таблицы 3.2, выполнить необходимый пересчет параметров элементов фильтра.
В таблице 3.2 даны значения емкостей (в фарадах) для схемы повторителя в зависимости от числа полюсов фильтра. При этом для получения фильтра, например, четвертого порядка, используют каскадное включение двух одинаковых повторителей, но элементы первого каскада рассчитывают как для фильтра с двумя полюсами, а второго каскада – как для фильтра с четырьмя полюсами.

Рисунок 3.30 – Амплитудно-частотные характеристики ФНЧ (слева) и ФВЧ (справа) Баттерворта
Таблица 3.2 – Величины емкостей конденсаторов (фарад)
| Число полюсов | Фильтр Бесселя | Фильтр Баттерворта | ||
| C1 | С2 | C1 | С2 | |
| 0,9066 | 0,6799 | 1,414 | 0,7071 | |
| 0,7351 1,0120 | 0,6746 0,3900 | 1,082 2,613 | 0,9241 0,3825 | |
| 0,6352 0,7225 1,0730 | 0,6098 0,4835 0,2561 | 1,035 1,414 3,863 | 0,9660 0,7071 0,2588 | |
| 0,5673 0,6090 0,7257 1,1160 | 0,5539 0,4861 0,3590 0,1857 | 1,091 1,202 1,800 5,125 | 0,9809 0,8313 0,5557 0,1950 | |
| 0,5172 0,5412 0,5999 0,7326 1,1510 | 0,5092 0,4682 0,3896 0,2792 0,1437 | 1,012 1,122 1,414 2,202 6,389 | 0,9874 0,8908 0,7071 0,4540 0,1563 |
На рисунке 3.31 показана процедура расчета схем фильтров на повторителях на примере двухполюсных ФНЧ (слева) и ФВЧ (справа) Баттерворта с частотой среза fв = 1 кГц.
Величины компонентов, взятые из таблицы 3.2, для схемы ФНЧ нормированы для частоты 1 рад/с при сопротивлении резисторов 1 Ом и емкости конденсаторов в фарадах. Емкости конденсаторов фильтра пересчитываются по частоте делением величин емкостей, взятых из таблицы, на частоту среза в радианах (2pfв). Компоненты фильтра пересчитывают умножением величин сопротивлений на подходящий коэффициент (например, 104) и делением величин емкостей на тот же коэффициент. В результате получаем следующие значения параметров элементов ФНЧ: С1 = 0,0225 мкФ, С2 = 0,0112 мкФ, R1 = R2 = 10 кОм.
Величины компонентов, взятые из таблицы 3.2, для схемы ФВЧ нормированы для частоты 1 рад/с при емкости конденсаторов 1 Ф и сопротивлении резисторов в омах, обратных значениям емкостей. Емкости конденсаторов фильтра пересчитываются по частоте делением величин емкостей на частоту среза в радианах (2pfн). Компоненты фильтра пересчитывают умножением величин сопротивлений на подходящий коэффициент (например, 14,1 103) и делением величин емкостей на тот же коэффициент. В результате получаем следующие значения параметров элементов ФВЧ: С1 = С2 = 0,0113 мкФ, R1 = 10 кОм, R2 = 20 кОм.
Полосовой и режекторный фильтры
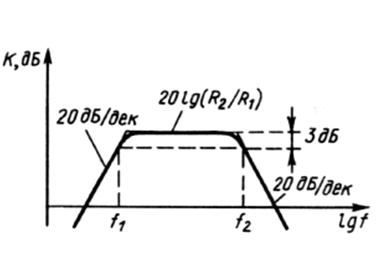
Простейший полосовой фильтр может быть получен посредством объединения фильтров нижних и верхних частот (например, интегратора и дифференциатора). Пример такой схемы показан на рисунке 3.32, а, а его логарифмическая АЧХ – на рисунке 3.32, б.
Частоты среза фильтра определяются из выражений:
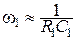 , (3.42)
, (3.42)
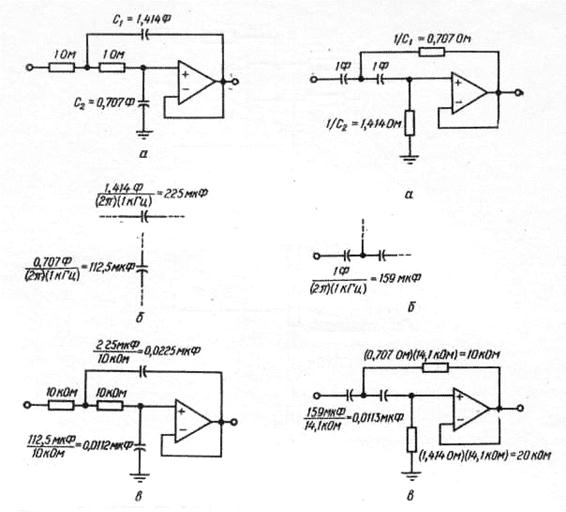
Рисунок 3.31 – Последовательность расчета ФНЧ (слева) и ФВЧ (справа)
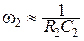 . (3.43)
. (3.43)
Для измерительной техники и техники обработки сигналов представляют интерес три типа схем ПФ:
— фильтр с многопетлевой обратной связью – применяется при величинах добротности до 10 и выгодно отличается от других схем тем, что имеет всего лишь один операционный усилитель;
— биквадратный резонатор – является более сложным электрическим фильтром, выполняемым на трех ОУ и обеспечивающим добротность до 200;
— коммутируемый фильтр – обеспечивает добротность до 1000, необходимую при селекции узкополосных сигналов.
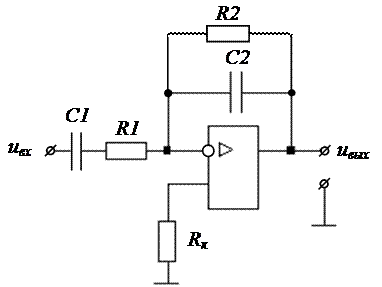
а
б
Рисунок 3.32 – Схема и логарифмическая АЧХ полосового фильтра
Добротность Q во всех случаях определяется следующим отношением
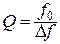 , (3.44)
, (3.44)
где f0 – средняя частота полосы пропускания;
Df – ширина полосы пропускания на уровне –3 дБ (то есть на уровне 0,707KUмакс).
АЧХ полосовых фильтров для различных значений Q приведены на рисунке 3.33.
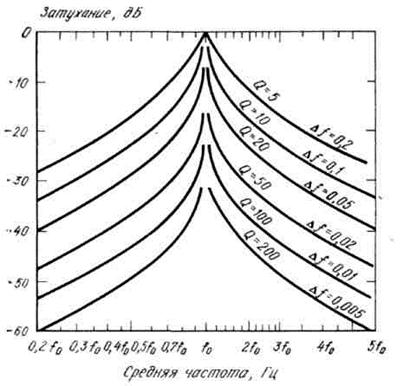 |
Рисунок 3.33 – АЧХ полосовых фильтров при разных значениях добротности
На рисунке 3.34 показана схема полосового фильтра с многопетлевой ОС (ПФМОС) и вид его АЧХ.
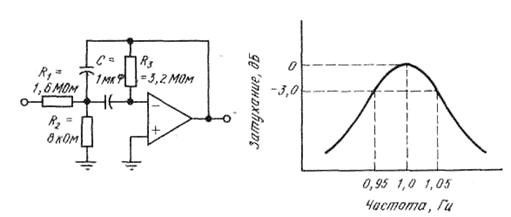
Рисунок 3.34 – Полосовой фильтр с многопетлевой обратной связью
Сопротивления резисторов R1, R2 и R3 ПФМОС при заданной емкости конденсаторов С = 1 мкФ, выбирают с учетом требуемой добротности Q и средней частоты f0 по формулам:
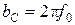 , (3.45)
, (3.45)
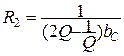 , (3.46)
, (3.46)
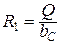 , (3.47)
, (3.47)
 . (3.48)
. (3.48)
Чтобы получить максимальную стабильность фильтра, расчет ведется для единичного усиления на частоте f0.
Полосовой фильтр второго порядка может быть выполнен по схеме, показанной на рисунке 3.45.
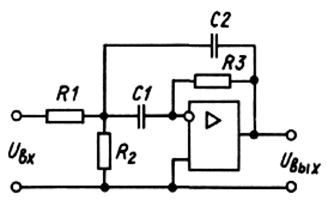
Рисунок 3.45 – Полосовой фильтр второго порядка
Квазирезонансная частота ПФ второго порядка (на которой коэффициент передачи фильтра максимален) может быть найдена из выражения
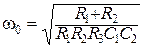 . (3.49)
. (3.49)
Режекторный фильтр может быть получен на основе схемы ПФМОС, если к ее выходу подключить неинвертирующий сумматор (рисунок 3.46). В такой схеме выделенный на частоте f0 сигнал c выхода инвертирующего ПФМОС, коэффициент усиления напряжения которого равен единице, поступает на один из входов неинвертирующего сумматора. Входной широкополосный сигнал поступает на второй вход сумматора также без усиления и без изменения фазы. В результате сложения двух сигналов в противофазе происходит подавление сигнала в области частоты режекции f0, то есть обеспечивается требуемый вид АЧХ для режекторного фильтра.
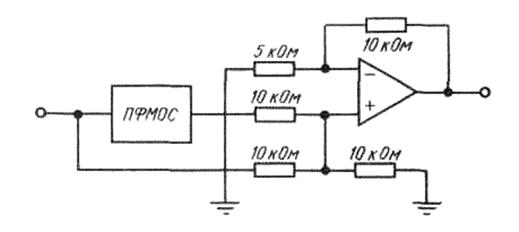
Рисунок 3.46 – Режекторный фильтр на основе схемы ПФМОС
Нужно отметить, что выше рассмотрены только отдельные примеры построения схем активных фильтров. На практике широко применяются также схемы, основу которых составляют мост Вина или двойной Т-мост.
РадиоКот >Статьи >
| Теги статьи: | Добавить тег |
Практическое применение операционных усилителей.Часть вторая.
Часть вторая.
Итак, в первой части мы рассмотрели схемы включения ОУ в качестве усилителей, в этой части рассмотрим включения ОУ в качестве фильтров.
Фильтр Высоких Частот (ФВЧ, High-Pass — как угодно)
Требуется он для отсекания сигнала, частота которого ниже определенного порога, который называется, кстати, частотой среза.
Простейший ФВЧ выглядит так:
Первая схема с неинвертирующим включением ОУ, вторая — с инвертирующим.
Это фильтр первого порядка с ослаблением ненужного сигнала — крутизной — 6дБ на октаву. Определить частоту среза можно, рассчитывая реактивное сопротивление конденсатора. Когда оно станет равным сопротивлению резистора, включенного последовательно с конденсатором — это будет самое то.
Формула следующая:
Где F — частота в Герцах, C — емкость в Фарадах, Ec — сопротивление в Омах.
Если крутизна фильтра первого порядка кажется недостаточной, можно справить фильтр второго порядка — с крутизной 12 дБ на октаву как показано на рисунке.
Это — так называемый, фильтр Баттерворта. Назван так, в честь товарища Баттерворта, который изобрел много чего математического, в том числе функции полиномиального вида, которыми впоследствии физики описали АЧХ и прочие физические проявления природы. (Спасибо Оля-ля за уточнение личности гражданина Баттерворта.)
Чтобы посчитать его граничную частоту можно воспользоваться следующими соотношениями:
R1=R2; С1=2С2;
При выборе резисторов надо учесть, что их номиналы должны лежать в пределах 10-100 кОм, поскольку выходное сопротивление фильтра растет вместе с частотой и если номиналы резисторов выходят за вышеуказанные рамки это может сказаться на работе фильтра. Отрицательно, разумеется — иначе зачем предупреждать?
Фильтр Низких Частот (ФНЧ, Low-Pass — как угодно)
Работа этого фильтра прямо противоположна предыдущему — он отрезает сигнал, частота которого выше частоты среза. В принципе, все то же самое, что и в предыдущем случае, только конденсатор включается не последовательно с резистором, а параллельно ему.
Первая схема — неинвертирующее включение, вторая — инвертирующее. Частота среза считается ровно таким же способом, как и в случае ФВЧ.
Ну и схема фильтра второго порядка — того же самого гражданина Баттерворта.
Опять же — считается все точно так же, как было описано выше.
Полосовой Фильтр (Band-Pass)
Полосовой фильтр применяется в тех случаях, когда необходимо выделить некую полосу частот из всего спектра. Например, в спектроанализаторах или вроде того.
Формулы расчета приводить тут не буду — дюже они забористые. Для расчета полосовых фильтром советую воспользоваться замечательной программой — Filter Wiz Pro от Schematica Software. Впрочем, ей так же можно воспользоваться и для расчетов любых других фильтров.
Фильтр-пробка (Notch Filter)
Если вам нужно ослабить (практически до нуля) некую выбранную частоту, то это фильтр как раз для вас.
Формула расчета вот такая:
где R=R3=R4, C=C1=C2;
При построении этого фильтра очень важна точность номиналов компонентов — от этого зависит степень «убивания» выбранной частоты. Так, при применении резисторов и конденсаторов с допуском 1%, можно получить ослабление частоты до 45дБ, хотя, теоретически, можно добиться и 60дБ. Например, если вы хотите грохнуть ненавистную всем частоту 50Гц, то берем следующие номиналы: R1=R2=10кОм, R3=R4=68кОм, С1=С2=47нФ.
Фильтр-пробка с двойным Т-мостом.
С помощью этого фильтра можно не только ослаблять выбранную частот, но и регулировать степень её ослабления переменным резистором R4. Формула расчета номиналов такая же, как и в предыдущем случае.
С фильтрами все, в следующей части еще кое-что интересное.
Вопросы, как обычно, складываем .
|
Как вам эта статья? |
Заработало ли это устройство у вас? |
||||||
|
|
Фильтр верхних частот
Схема фильтра высоких частот второго порядка показана на Рис. 22.
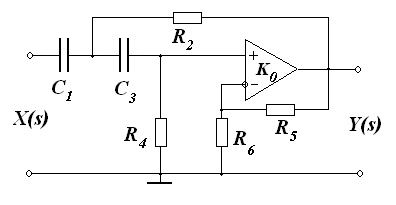
Рис. 22. Активный фильтр высоких частот.
Выражение для коэффициента передачи такого фильтра записывается как:
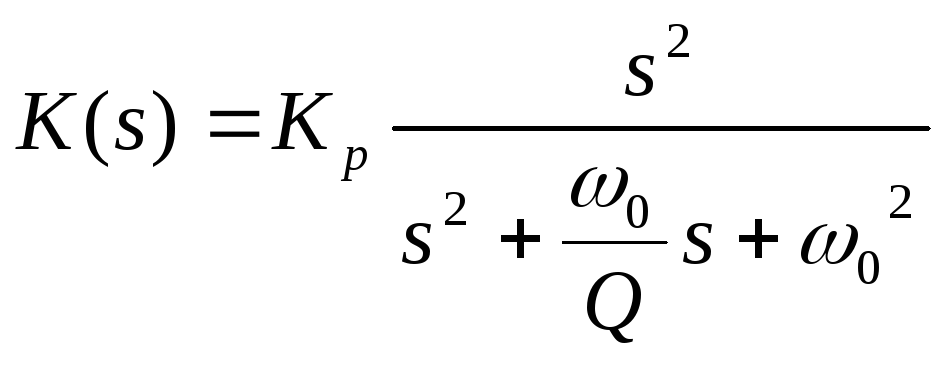 , (7)
, (7)
где при К0 >> 1
![]() ,
,![]() ,
,
 .
.
Если R2 = R4 = R и C1 = C3 = С, то коэффициент передачи можно записать как
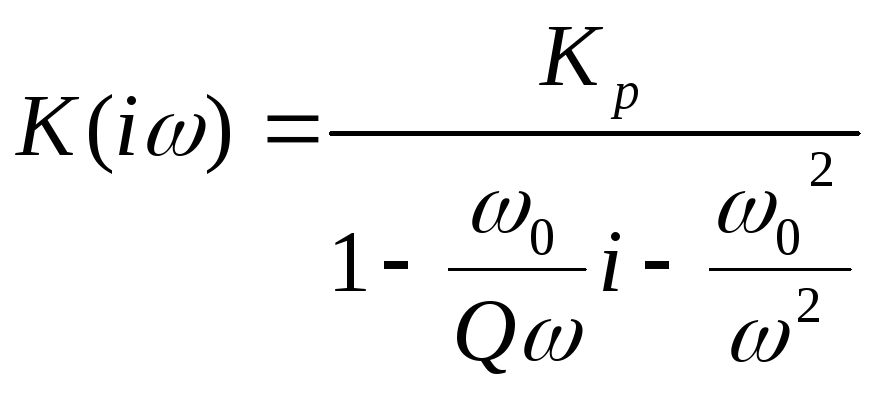
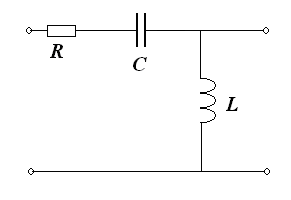
Схема пассивного фильтра высоких частот второго порядка на RLC-элементах с аналогичной частотной характеристикой приведена на Рис. 23.
|
|
Коэффициент передачи такого фильтра описывается выражением (7) со следующими значениями параметров:
|
|
Рис. 23. Схема пассивного фильтра высоких частот второго порядка. |
|
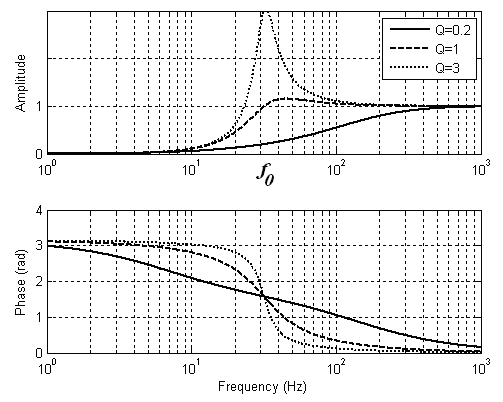
Рис. 24. АЧХ и ФЧХ активного RC-фильтра высоких частот второго порядка.
Исследовать АЧХ и ФЧХ рассматриваемого фильтра можно также, как и в предыдущем случае в Simulink. Для параметров электрической схемы Кр = 1, ω0 = 200 рад/с вектор числителя передаточной функции будет b = и вектор знаменателя a = . Зависимость частотных характеристик от величины параметра Q показаны на Рис 24. В этом случае также параметры схемы подобраны так, чтобы собственная частота системы ω0 = 200 рад/с. После перевода в герцы f0 = 31.8310. Здесь также с увеличением Q АЧХ активного фильтра приобретает резонансный характер.
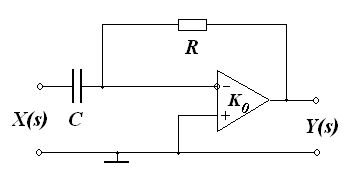
Активный фильтр высоких частот первого порядка изображен на Рис. 25., а его пассивный аналог – на Рис. 26.
|
|
Коэффициент передачи активного фильтра первого порядка равен:
|
|
Рис. 25. Активный фильтр первого порядка высоких частот. |
|
|
|
Коэффициент передачи пассивного фильтра: |
|
Рис. 26. Пассивный фильтр первого порядка высоких частот. |
|
Сравнивая приведенные выражения для коэффициентов передачи видим, что при одинаковых постоянных τ’1 и τ модуль коэффициента передачи активного фильтра в К0 раз больше, чем у пассивного.
Частотные характеристики активного фильтра высоких частот приведены на Рис 27. (для τ = 1с).
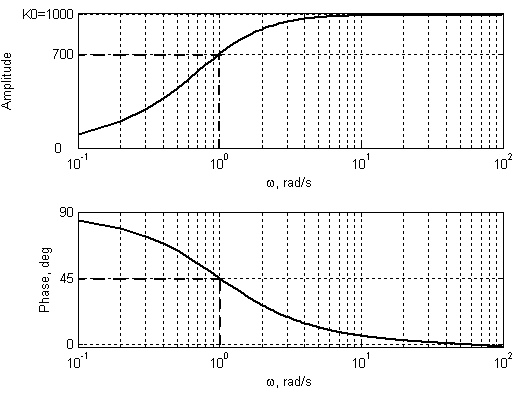
Рис. 27. АЧХ и ФЧХ активного фильтра высоких частот (для τ = 1с).
Режекторный фильтр
Режекторный фильтр с регулируемой полосой режекции может быть построен по схеме, приведенной на Рис. 28.
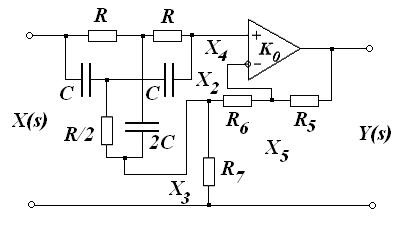
Рис. 28. Режекторный активный фильтр.
В этой схеме в цепи частотноизбирательной обратной связи включен сбалансированный двойной Т-образный RC-мост (Рис. 29).
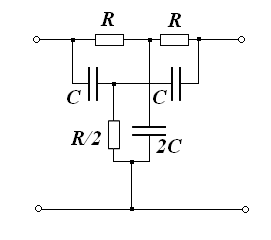
Рис. 29. Сбалансированный двойной Т-образный RC-мост.
Коэффициент передачи Т-образного RC-моста в предположении, что мост не нагружен, равен
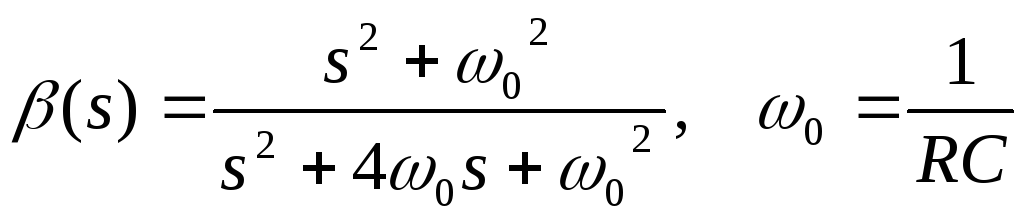 . (9)
. (9)
Такое приближение может быть принято, т.к. входное сопротивление усилителя велико. Коэффициент передачи режекторного фильтра можно определить как:
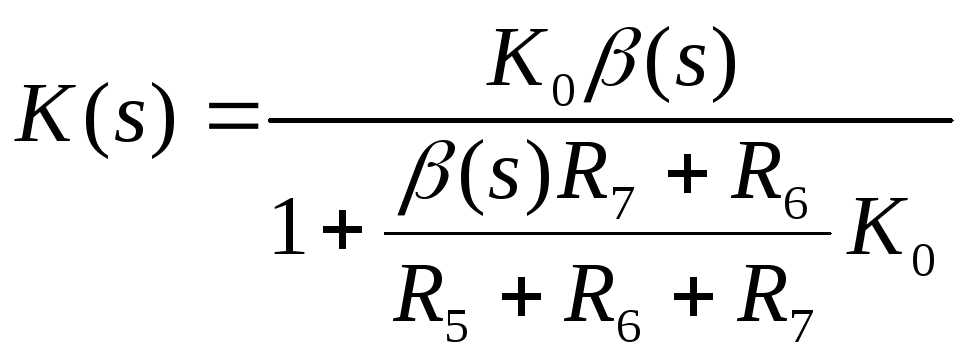 .
.
Выделим выражения, описывающие величину усиления, регулируемую соотношением сопротивлений в цепи обратной связи:
 .
.
Тогда коэффициент передачи можно переписать как:
![]() .
.
Используя выражение для β(s), получим
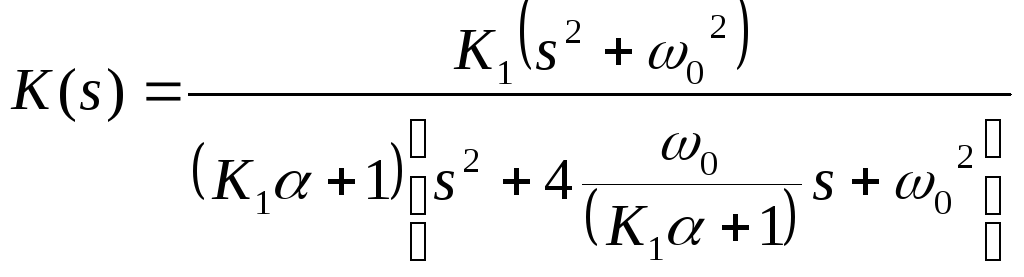 .
.
Если ![]() , то
, то![]() . Таким образом, в этом случае коэффициент передачи фильтра не зависит отК0 и определяется выражением
. Таким образом, в этом случае коэффициент передачи фильтра не зависит отК0 и определяется выражением
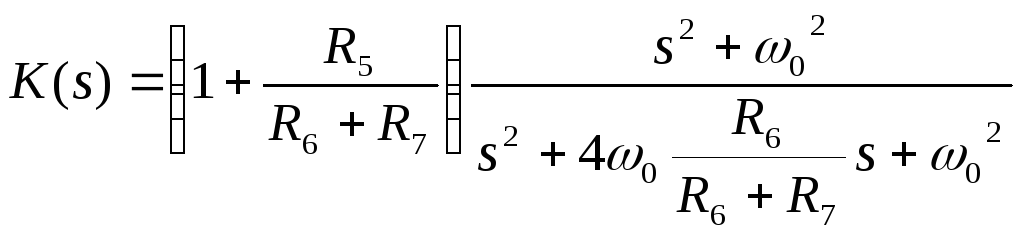 . (10)
. (10)
Введя обозначения
![]() ,
,
приведем это выражение к стандартному виду
 .
.
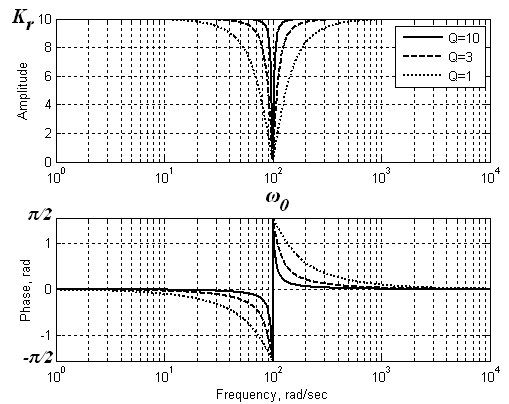
Рис. 29. АЧХ и ФЧХ активного режекторного RC-фильтра.
Семейство АЧХ и ФЧХ активного режекторного RC-фильтра при различных значениях Q приведены на (Рис. 29). Здесь для определенности выбраны значения Kr = 10, ω0 = 100 рад/с.
Полоса режекции определяется величиной Q и оказывается тем более узкой, чем больше Q. Существенно, что при любых значениях Кr режекторный активный фильтр остается устойчивым, т.к. всегда Q больше нуля. Если мост не сбалансирован (не точно выполняются соотношения между R и C в вертикальных и горизонтальных плечах моста (Рис.)), то режекция не является полной.
На Рис. 30. изображены характеристики для сбалансированного (пунктирная линия) и несбалансированного (сплошная линия) моста. Заметим, что мы описывали эту схему в предположении, что Т-образный мост не нагружен. Поэтому, для того чтобы результаты согласовывались с теоретическими результатами, выходное сопротивление Т-образного моста должно быть много меньше входного сопротивления усилителя и одновременно много больше сопротивления R7, через которое средняя точка моста подключена к земле.
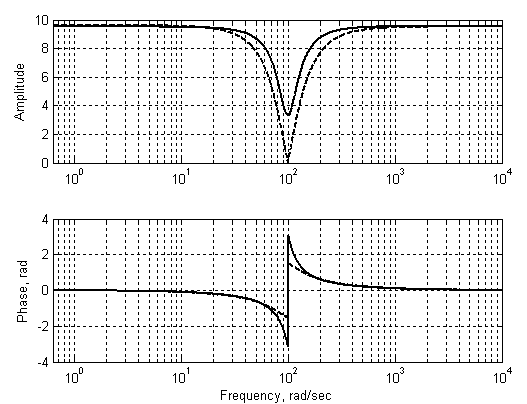
Рис. 30. АЧХ и ФЧХ для сбалансированного и несбалансированного моста.
Модель активного режекторного RC-фильтра в SPS будет выглядеть, как показано на Рис 31.
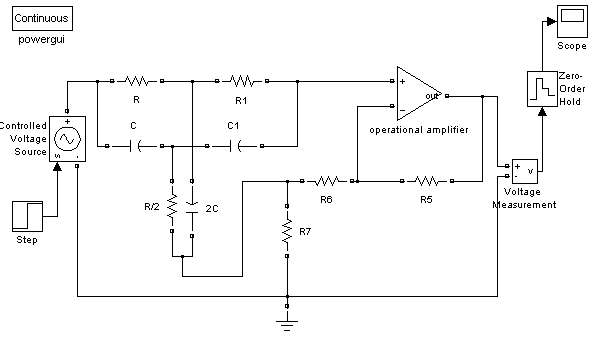
Рис. 31. Модель активного режекторного RC-фильтра в SPS.
 Фильтр низких частот первого порядка
Фильтр низких частот первого порядка
На схеме показан активный фильтр низких частот. Он состоит из RC-фильтра низких частот, подключенного ко входу неинвертирующего операционного усилителя (ОУ). Усилитель подключен как повторитель напряжения с коэффициентом усиления по постоянному току равному единице Av = +1.
Преимущество данной схемы заключается в том, что высокое полное входное сопротивление ОУ защищает фильтр от чрезмерной нагрузки нагрузки на выходе, а низкое полное выходное сопротивление не дает сдвигаться частоте среза от изменения сопротивления нагрузки.
Хотя эта схема обеспечивает хорошую стабильность фильтру, ее основным недостатком является то, что она не дает коэффициент усиления по напряжению выше единицы. Хотя коэффициент усиления по напряжению и равен 1, усиление по мощности намного больше единицы, а выходное сопротивление значительно ниже входного. Если требуется коэффициент усиления по напряжению больше единицы используется схема представленная на следующем рисунке.
 Активный фильтр низких частот с усилением
Активный фильтр низких частот с усилением
Частотная характеристика контура будет такой же как и для пассивного RC-фильтра, за исключением того, что амплитуда выходного сигнала в полосе пропускания увеличивается на коэффициент усиления AF. Для неинвертирующего ОУ коэффициент усиления по напряжению задается отношением сопротивления R2 к R1 и рассчитывается по формуле:
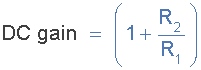
Усиление для фильтра низких частот первого порядка рассчитывается по формуле:
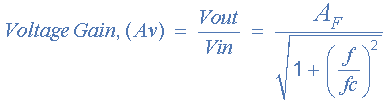
где:
AF — усиление в полосе пропускания фильтра (1 + R2/R1);
ƒ — частота входного сигнала в герцах;
ƒc — частота среза в герцах;
Коэффициент усиления будет изменяться в зависимости от частоты, подаваемой на фильтр:
1. На очень низких частотах, ƒ < ƒc
![]()
2. На частоте равной частоте среза, ƒ = ƒc
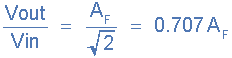
3. На очень высоких частотах, ƒ > ƒc
![]()
Из данных формул видно, что активный фильтр низких частот имеет практически постоянный коэффициент усиления на частотах от 0 Гц до частоты среза. На частоте равной ƒc коэффициент усиления будет равен 0.707AF . Далее при повышении частоты, коэффициент усиления будет уменьшаться с постоянной скоростью. Таким образом, если увеличить частоту в 10 раз, коэффициент усиления уменьшиться в 10 раз.
Другими словами коэффициент усиления уменьшается на 20 дБ (= 20log 10), каждый раз когда частота увеличивается в 10 раз. При работе с фильтрами величина усиления в полосе пропускания обычно выражается в дБ и рассчитываются по формулам:
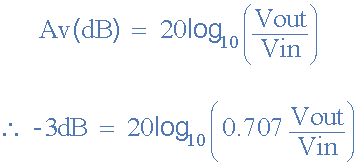
Из примера видно, что коэффициент усиления на частоте среза будет равен -3 дБ.
Пример расчета активного фильтра низких частот
К примеру нам нужно спроектировать неинвертирующий активный фильтр низких частот с коэффициентом усиления равным 10, частотой среза 159 Гц и полным входным сопротивлением 10 кОм.
Коэффициент усиления по напряжению для неинвертирующего операционного усилителя задается как:
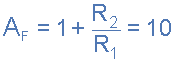
Предположим что значение резистора R1 = 1 кОм, тогда можно вычислить значение R2:
![]()
Для усиления по напряжению в 10 раз нам потребуются резисторы R1 = 1 кОм и R2 = 9 кОм. Однако резистора с номиналом 9 кОм не существует, выберем ближайшее стандартное значение 9.1 кОм.
Коэффициент усиления в дБ рассчитывается по формуле:
![]()
Частота среза рассчитывается по формуле:
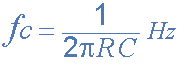
где, ƒc = 159 Гц и R = 10 кОм.
Подставляя значения в формулу выше можно вычислить емкость конденсатора C :
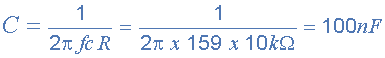
Окончательная схема и амплитудно-частотная характеристика представлены ниже.
Активные фильтры
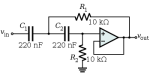 Электрическим фильтром называется устройство для передачи электрических сигналов, пропускающее токи в определенной области частот и препятствующее их прохождению вне этой области. В радиотехнике и электронике электрические фильтры подразделяют на пассивные и активные. Схемы пассивных фильтров содержат только пассивные элементы: резисторы, конденсаторы и катушки индуктивности.
Электрическим фильтром называется устройство для передачи электрических сигналов, пропускающее токи в определенной области частот и препятствующее их прохождению вне этой области. В радиотехнике и электронике электрические фильтры подразделяют на пассивные и активные. Схемы пассивных фильтров содержат только пассивные элементы: резисторы, конденсаторы и катушки индуктивности.
В схемы активных фильтров помимо указанных элементов входят такие активные изделия, как транзисторы или интегральные микросхемы. Фильтрующие свойства устройства определяются его амплитудно-частотной характеристикой, которой называется зависимость коэффициента усиления этого устройства от частоты сигнала. В некоторой области частот, которая называется полосой пропускания или полосой прозрачности, электрические колебания передаются фильтром с входа на выход практически без ослабления. Вне полосы прозрачности расположена полоса затухания или задерживания, в пределах которой частотные составляющие сигнала ослабляются. Между полосой прозрачности и полосой задерживания находится частота, называемая граничной. В связи с тем что существует плавный переход между полосой прозрачности и полосой затухания, граничной обычно считается частота, на которой ослабление сигнала оказывается равным -3 дБ — то есть по напряжению в √2 раз меньше, чем в полосе прозрачности.
Всегда интересно получить крутой переход амплитудно-частотной характеристики между полосой прозрачности и полосой затухания. В пассивных фильтрах увеличения крутизны такого перехода добиваются усложнением схемы и применением многозвенных систем. Сложные фильтры требуют громоздких расчетов и точной настройки. Активные фильтры благодаря использованию обратной связи оказываются значительно проще и дешевле.
Принято подразделять фильтры на четыре категории в зависимости от расположения полосы прозрачности:
• фильтры нижних частот (0 ≤ f ≤ f0);
• фильтры верхних частот (f ≥ f0);
• полосовые фильтры (f01 ≤ f ≤ f02);
• заграждающие или режекторные фильтры (0 ≤ f ≤ f01 и f ≥ f02).
Здесь f — частота сигналов, проходящих через фильтр; f0 -граничная частота; f01 — нижняя граничная частота; f02 — верхняя граничная частота. Таким образом, фильтр нижних частот nponycкает составляющие сигнала, частота которых меньше граничной частоты; фильтр верхних частот пропускает составляющие сигнала, частота которых больше граничной частоты; полосовой фильтр пропускает составляющие сигнала, частота которых находится между нижней граничной частотой f01 и верхней граничной частотой f02; наконец режекторный фильтр ослабляет сигналы, частота которых находится между нижней граничной f01 и верхней граничной f02 частотами. Существуют и более сложные фильтры специального назначения, например гребенчатый фильтр, применяемый в цветном телевидении, пропускающий много узких полос и ослабляющий промежутки между ними.
Электрические фильтры находят широкое применение в электротехнике, радиотехнике и электронике. Так на выходе выпрямителей используется фильтр нижних частот, пропускающий только постоянную составляющую выпрямленного тока и ослабляющий прохождение пульсаций. В радиоприемниках широко используются полосовые фильтры, которые позволяют выделить из принятых антенной сигналов множества радиостанций только один, полоса частот которого оказывается в полосе прозрачности фильтра.
Принято еще одно деление всех фильтров на две категории: фильтры, схема которых содержит катушки индуктивности, и фильтры без индуктивностей, RC-фильтры или резисторно-конденсаторные фильтры.
Активные резисторно-конденсаторные фильтры имеют огромное преимущество перед их пассивными аналогами, особенно на частотах ниже 10 кГц. Пассивные фильтры для низких частот должны содержать катушки большой индуктивности и конденсаторы большой емкости. Поэтому они получаются громоздкими, дорогостоящими, а их характеристики оказываются далеко не идеальными.
Большая индуктивность достигается за счет большого числа витков катушки и применения ферромагнитного сердечника. Это лишает ее свойств чистой индуктивности, так как длинный провод многовитковой катушки обладает заметным сопротивлением, а ферромагнитный сердечник подвержен влиянию температуры на его магнитные свойства. Необходимость же использования большой емкости вынуждает применять конденсаторы, обладающие плохой стабильностью, например электролитические. Активные фильтры в значительной мере лишены указанных недостатков.
Схемы дифференциатора и интегратора, построенные с применением операционных усилителей, представляют собой простейшие активные фильтры. При выборе элементов схемы в определенной зависимости от частоты дифференциатор становится фильтром верхних частот, а интегратор — фильтром нижних частот. Далее будут рассмотрены примеры других более сложных и наиболее универсальных фильтров. Большое количество других возможных схем активных фильтров вместе с их детальным математическим анализом можно найти в разных учебниках и пособиях.
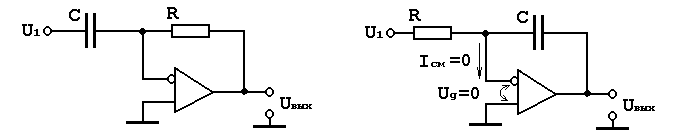
Фильтры нижних частот
Если объединить схему инвертирующего усилителя со схемой интегратора, образуется схема фильтра нижних частот первого порядка, которая показана на рис. 1.
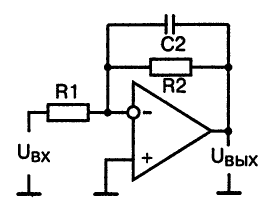
Рис. 1. Схема активного фильтра нижних частот первого порядка
Такой фильтр представляет собой инвертирующий усилитель, обладающий постоянным коэффициентом усиления в полосе прозрачности от постоянного тока до граничной частоты f0. Видно, что в пределах полосы прозрачности, пока емкостное сопротивление конденсатора достаточно велико, коэффициент усиления схемы совпадает с коэффициентом усиления инвертирующего усилителя:
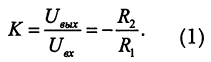
Граничная частота этого фильтра определяется элементами цепи обратной связи в соответствии с выражением:
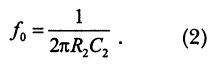
Амплитудно-частотная характеристика — зависимость амплитуды сигнала на выходе устройства от частоты при постоянной амплитуде на входе этого устройства — представлена на рис.2.
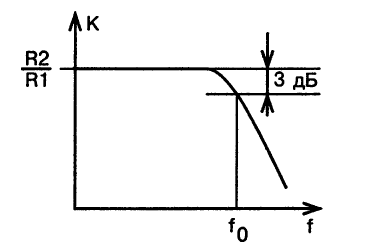
Рис. 2. Амплитудно-частотная характеристика фильтра нижних частот первого порядка
В полосе затухания выше граничной частоты f0 усиление уменьшается с интенсивностью 20 дБ/декада (или 6 дБ/октава), что означает уменьшение коэффициента усиления по напряжению в 10 раз при увеличении частоты также в 10 раз или уменьшение коэффициента усиления в два раза при каждом удвоении частоты.
Если такой крутизны наклона амплитудно-частотной характеристики в полосе затухания недостаточно, можно использовать фильтр нижних частот второго порядка, схема которого показана на рис.З.
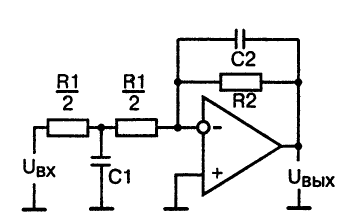
Рис. З. Принципиальная схема активного фильтра нижних частот второго порядка
Коэффициент усиления фильтра нижних частот второго порядка такой же, как у фильтра первого порядка, в связи с тем что суммарное сопротивление резисторов в цепи инверсного входа, как и ранее, выражается значением R1:
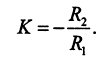
Граничная частота при выполнении условия R1C1 = 4R2C2 также выражается прежней формулой:
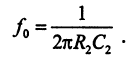
Что касается амплитудно-частотной характеристики этого фильтра, представленной на рис. 4, то она отличается повышенной крутизной наклона, которая составляет 12 дБ/октава.
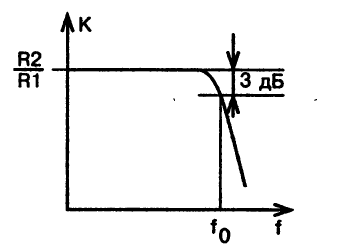
Рис. 4. Амплитудно-частотная характеристика фильтра нижних частот второго порядка
Таким образом, в полосе затухания при увеличении частоты вдвое напряжение сигнала на выходе фильтра уменьшается в четыре раза.
Фильтры верхних частот
Аналогично построена схема фильтра верхних частот, которая представлена на рис.5. Такой фильтр является инвертирующим усилителем с постоянным коэффициентом усиления в полосе прозрачности от частоты f0 и более. В полосе прозрачности коэффициент усиления схемы такой же, как у инвертирующего усилителя:
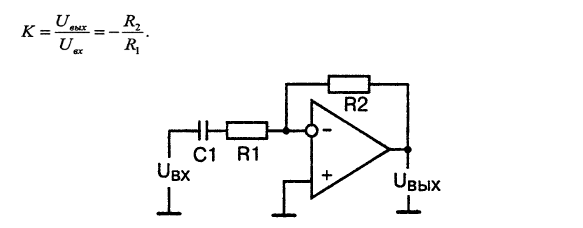
Рис.5. Принципиальная схема активного фильтра верхних частот первого порядка
Граничная частота f0 на уровне -3 дБ задается входной цепью в соответствии с выражением:
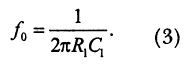
Крутизна наклона амплитудно-частотной характеристики, которая представлена на рис.6, в области граничной частоты составляет 6 дБ/октава.
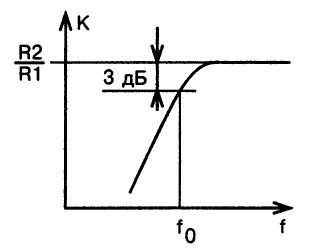
Рис.6. Амплитудно-частотная характеристика фильтра верхних частот первого порядка
Как и в случае фильтров нижних частот, можно собрать активный фильтр верхних частот второго порядка в целях повышенного подавления сигнала в полосе затухания. Принципиальная схема такого фильтра показана на рис.7.
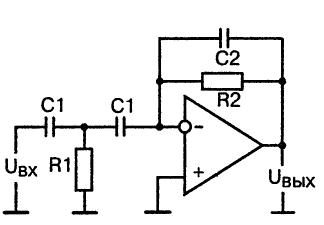
Рис.7. Принципиальная схема активного фильтра верхних частот второго порядка
Крутизна наклона амплитудно-частотной характеристики фильтра верхних частот второго порядка в области граничной частоты составляет 12 дБ/октава, а сама характеристика показана на рис.8.
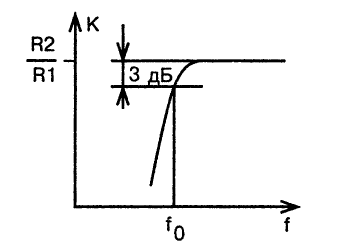
Рис.8. Амплитудно-частотная характеристика фильтра верхних частот второго порядка
Полосовые фильтры
Если объединить активный фильтр нижних частот с активным фильтром верхних частот, то в результате образуется полосовой фильтр, принципиальная схема которого приведена на рис.9.
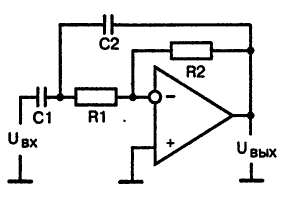
Рис. 9. Принципиальная схема активного полосового фильтра
Эту схему иногда называют избирательным усилителем с ин-тегродифференцирующей обратной связью. Подобно усилителям, содержащим колебательные контуры, полосовой фильтр также имеет амплитудно-частотную характеристику с выраженным максимумом на определенной частоте. Называть такую частоту резонансной нельзя, так как резонанс возможен только в контурах, образованных индуктивностью и емкостью. В других случаях частоту такого максимума обычно называют частотой квазирезонанса. Для рассматриваемого полосового фильтра частота квазирезонанса f0 определяется элементами цепи обратной связи:
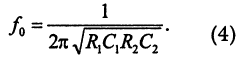
Амплитудно-частотная характеристика этого полосового фильтра показана на рис. 10.
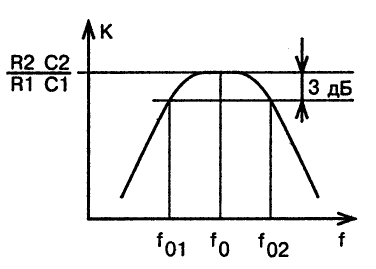
Рис.10. Амплитудно-частотная характеристика полосового фильтра
Максимальный коэффициент усиления на частоте квазирезонанса оказывается равным:
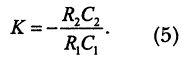
Относительная полоса пропускания на уровне -3 дБ:
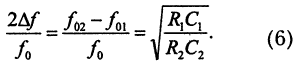
Принципиальная схема еще одного полосового фильтра приведена на рис. 11.
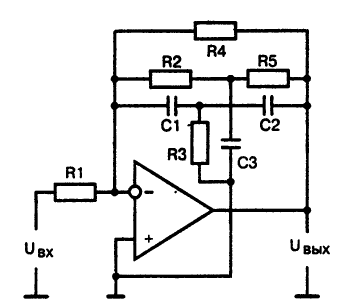
Рис. 11. Принципиальная схема полосового фильтра с двойным Т-фильтром
Здесь в цепь отрицательной обратной связи включен двойной Т-фильтр, образованный резисторами R2, R3, R5 и конденсаторами Cl, С2, СЗ.
Как известно, если выполняются следующие условия: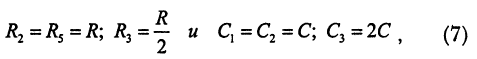
амплитудно-частотная характеристика двойного Т-фильтра содержит квазирезонанс, частота которого равна
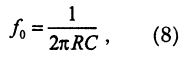
причем на частоте квазирезонанса коэффициент передачи двойного Т-фильтра равен нулю. Поэтому активный фильтр с двойным Т-фильтром, включенным в цепь отрицательной обратной связи, является полосовым фильтром с максимумом амплитудно-частотной характеристики на частоте квазирезонанса. Три такие характеристики представлены на рис. 12. Характеристики различаются разными сопротивлениями резистора R4: нижняя соответствует R4 = 100 кОм, средняя — R4 = 1 МОм, верхняя — R4 = ∞.
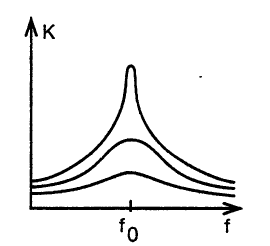
Рис. 12. Амплитудно-частотная характеристика активного фильтра с двойным Т-фильтром в цепи отрицательной обратной связи
Режекторные фильтры
Тот же самый двойной Т-фильтр может быть включен не в цепь отрицательной обратной связи, как это сделано при создании полосового фильтра, а в цепь входного сигнала. При этом образуется активный режекторный фильтр, схема которого приведена на рис, 13.
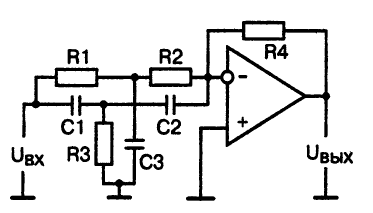
Рис.13. Принципиальная схема режекторного фильтра с двойным Т-фильтром
При выполнении прежних условий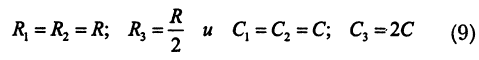
амплитудно-частотная характеристика активного фильтра, имеющего во входной цепи двойной Т-фильтр, содержит квазирезонанс, частота которого по-прежнему определяется фор мулой (8). Но на частоте квазирезонанса коэффициент усиления этого активного фильтра равен нулю. Амплитудно-частотная характеристика активного фильтра с двойным Т-фильтром во входной цепи показана на рис.14.
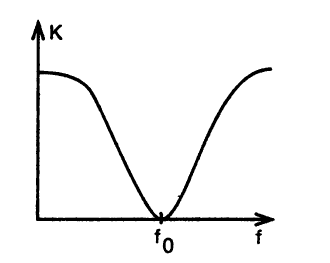
Рис. 14. Амплитудно-частотная характеристика активного фильтра с двойным Т-фильтром во входной цепи
Сложные фильтры
Несколько активных фильтров можно соединять последовательно для получения амплитудно-частотной характеристики с повышенной крутизной наклона. Кроме того, соединенные последовательно секции простых фильтров имеют пониженную чувствительность. Это означает, что небольшое отклонение величины одного из компонентов схемы (отклонение сопротивления резистора или емкости конденсатора от нормы) будет приводить к меньшему влиянию на окончательную характеристику фильтра, чем в случае аналогичного сложного фильтра, построенного на одном операционном усилителе.
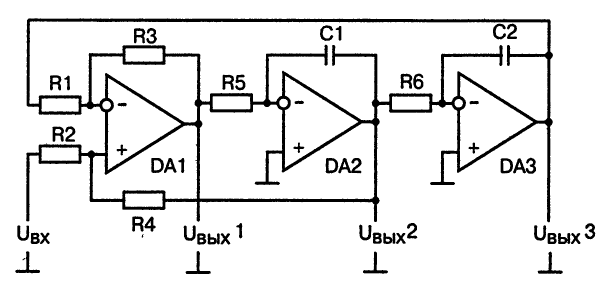
Рис. 15. Принципиальная схема ступенчатого фильтра
На рис. 15 показан ступенчатый фильтр, собранный из трех операционных усилителей. Популярность таких фильтров резко возросла после появления в продаже интегральных микросхем, содержащих несколько операционных усилителей в одном корпусе. Достоинствами этого фильтра являются низкая чувствительность к отклонениям величин компонентов и возможность получения трех выходов: верхних частот Uвых1, полосового Uвых2 и нижних частот UвыхЗ.
Фильтр составлен из суммирующего усилителя DA1 и двух интеграторов DA2, DA3, которые соединены в виде замкнутой петли. Если элементы схемы выбраны согласно условию![]()
то граничная частота оказывается равной
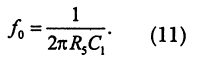
Выходы верхних и нижних частот имеют крутизну наклона амплитудно-частотной характеристики, равную 12 дБ/октава, а полосовой выход имеет треугольную характеристику с максимумом на частоте f0 с добротностью Q, которая определяется резисторами установки усиления микросхемы DA1.

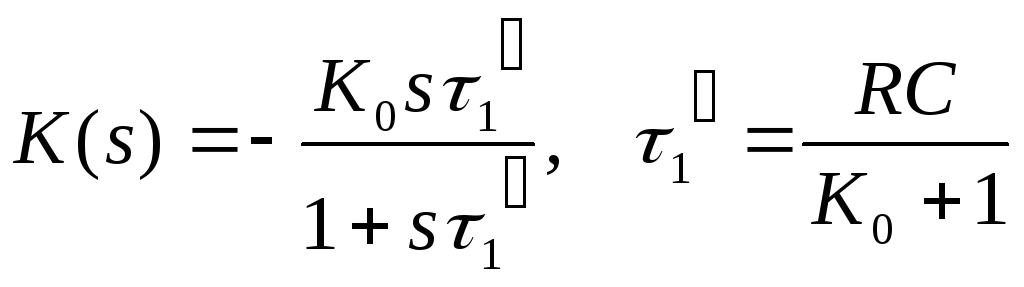 .(8)
.(8)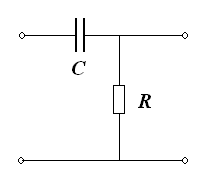


Добавить комментарий