Зачем всё это нужно?

Когда чайник, уперевшись в необходимость отойти от простой последовательности действий, задаёт на хабре вопрос типа «как сделать вот это?», ему с вероятностью 70% отвечают «погугли конечные автоматы» и 30% «используй finite state machine» в зависимости от страны работодателя профессионала. На следующий вопрос «а как?» отправляют в гугл. Идёт такой чайник, что только закончил мигать светодиодом и вытер пот со лба, что учил в школе немецкий и всю жизнь работал бульдозеристом в этот гугл и видит там статьи типа Википедия про конечные автоматы с формулами и в которых понятны только предлоги.

Так как я тоже чайник, но до бульдозера работал программистом 30 лет назад, наступив на множество граблей по мере освоения программирования микроконтроллеров, решил написать эту статью простым языком для начинающих.

Итак, задача стоит, например, научить ардуину понимать нажатие кнопки типа клик, нажатие и удержание, то есть, короткий тык в кнопку, длинный и очень длинный. Любой начинающий может сделать это в функции loop() и гордиться этим, но как быть, если кнопок несколько? А если при этом надо не мешать выполнению другого кода? Я написал библиотеку SmartButton для Arduino, чтобы потом не возвращаться к теме кнопок. Здесь же напишу, как она работает.

Немного теории

Так или иначе, но у вас есть объекты. Вы можете называть их кнопками, дисплеями, светодиодными лентами, роботами и измерителем уровня воды в бачке. Если ваш код выполняется не в одну ниточку последовательно, а по каким-то событиям, вы храните состояние объектов. Вы можете называть это как угодно, но это факт. Для кнопки есть, например, состояния «нажата» и «отпущена». Для робота, например: стоит, едет прямо, поворачивает. Количество этих состояний конечно. Ну, в нашем случае, да. Добавим состояния «клик», «нажатие» и «удержание». Уже пять состояний, которые нам надо различать. Причём, интересны нам лишь последние три. Этими пятью состояниями живёт кнопка. В страшном внешнем мире происходят события, которые от кнопки в общем-то никак не зависят: тыкания в неё пальцем, отпускания, удержания на разное время итп. Назовём их событие.

Итак, мы имеем объект «кнопка» у которого конечное количество состояний и на него действуют события. Это и есть конечный автомат (КА). В теории КА список возможных событий называют словарём, а события словами. Я дико извиняюсь, я это проходил 30 лет назад и плохо помню терминологию. Вам же не терминология нужна, правда?

В данной статье мы напишем замечательный код, который будет переводить наш КА из состояния в состояние в зависимости от событий. Он и является собственно машиной конечных автоматов (МКА).

Не обязательно всё ваше устройство запихивать в один огромный КА, можно разбить на отдельные объекты, каждый из которых обслуживается своей МКА и даже находится в отдельном файле кода. Многие свои объекты вы сможете поместить на GitHub в виде готовых библиотек ардуины и использовать потом не вникая в их реализацию.

Если ваш код не требует переносимости и повторного использования, можно всё лепить в один большой файл, что и делают как раз начинающие.

Практика

Основой проектирования МКА является таблица.

• По горизонтали пишем все-все возможные события.
• По вертикали все состояния.
• В клетках действия. Переход в новое состояние — это тоже действие.

Для кнопки это будет выглядеть вот так:

Состояние \ Событие	Нажата	Отпущена	Нажата 20мс	Нажата 250мс	Нажата 1с	Нажата 3с
Не Нажата
Кликнута
Нажата
Удержана
Слишком долго удержана

Зачем так сложно? Надо же описать все возможные состояния и учесть все возможные события.

События:

• Нажата — это когда мы обнаружили, что контакт замкнут.
• Отпущена — это когда выяснилось, что контакт разомкнут.
• Нажата 20мс — надо учесть дребезг контактов и игнорировать размыкание какое-то время, дальше уже считатется, что клик.
• Нажата 250мс — для клика 250мс достаточно, всё что дольше — это уже нажатие.
• Нажата 1с — больше 1с это уже удержание.
• нажата 3с — удержание больше 3с посчитаем ошибкой.

Время вы можете поставить своё, как вам удобно. Чтобы не менять потом в разных местах цифры, лучше сразу заменить их буквами 🙂

#define SmartButton_debounce 20 #define SmartButton_hold 250 #define SmartButton_long 1000 #define SmartButton_idle 3000

Состояния:

• Не нажата — рапортуем, что никто кнопочку не трогал.
• Дребезг — Ждём конец дребезга контактов.
• Кликнута — был клик.
• Нажата — кнопку нажали.
• Удержана — кнопку нажали и подержали.
• Слишком долго удержана — что-то пошло не так, предлагаю отказаться от нажатия в этом случае.

Итак, переводим русский язык на язык C++

// Нога контроллера для кнопки byte btPin; // События enum event {Press, Release, WaitDebounce, WaitHold, WaitLongHold, WaitIdle}; // Состояния enum state {Idle, PreClick, Click, Hold, LongHold, ForcedIdle}; // Текущее состояния enum state btState = Idle; // Время от нажатия кнопки unsigned long pressTimeStamp;

Обращу внимание, что и события и состояния указаны не как целая переменная типа byte или int, а как enum. Такая запись не столь любима профессионалами так как не даёт экономить биты столь дорогой в микроконтроллерах памяти, но, с другой стороны очень наглядна. При использовании enum нас не заботит каким числом закодирована каждая константа, мы пользуемся словами, а не числами.

Как расшифровать enum?

enum Имя {Константа, Константа, Константа};
Так мы создаём тип данных enum Имя, у которого есть набор фиксированных значений из тех, что в фигурных скобках. На самом деле, конечно же, это числовой целый тип, но значение констант нумеруется автоматически.
Можно указать значения и вручную:
enum Имя {КонстантаА=0, КонстантаБ=25};

Для объявления переменной такого нового типа можно написать так:
enum Имя Переменная;

В примере с кнопкой:

• enum event myEvent;
• enum state currentState;

Давайте уже заполним таблицу. Значком -> я обозначу переход в новое состояние.

Состояние \ Событие	Нажата	Отпущена	Нажата 20мс	Нажата 250мс	Нажата 1с	Нажата 3с
Не Нажата	->Дребезг	->Не Нажата
Дребезг		->Не Нажата	->Кликнута
Кликнута		->Не Нажата		->Нажата
Нажата		->Не Нажата			->Удержана
Удержана		->Не Нажата				->Слишком долго удержана
Слишком долго удержана		->Не Нажата

Для реализации таблицы мы сделаем функцию void doEvent(enum event e). Эта функция получает событие и выполняет действие как описано в таблице.

Откуда берутся события?

Настало время ненадолго покинуть нашу уютную кнопку и окунуться в ужасный внешний мир функции loop().

void loop() { // запоминаем текущий счётчик времени unsigned long mls = millis(); // генерим события // нажатие кнопки if (digitalRead(btPin)) doEvent(Press) else doEvent(Release) // ожидание дребезга прошло if (mls — pressTimeStamp > SmartButton_debounce) doEvent(WaitDebounce); // ожидание нажатия прошло if (mls — pressTimeStamp > SmartButton_hold) doEvent(WaitHold); // ожидание удержания прошло if (mls — pressTimeStamp > SmartButton_long) doEvent(WaitLongHold); // совсем перебор по времени if (mls — pressTimeStamp > SmartButton_idle) doEvent(WaitIdle); }

Итак, имея под рукой генератор событий, можно приступить к реализации МКА.

На самом деле, события могут генерироваться не только по подъёму уровня сигнала на ноге контроллера и по времени. События могут передаваться одним объектом другому. Например, вы хотите, чтобы нажатие одной кнопки автоматически «отпускало» другую. Для этого достаточно вызвать её doEvent() с параметром Release. МКА — это же не только кнопки. Превышение порога температуры является событием для МКА и вызывает включение вентилятора в теплице, к примеру. Датчик неисправности вентилятора меняет состояние теплицы на «аварийное» и так далее.

Три подхода к реализации таблицы в код

План-А: if {} elsif {} else {}

Это первое, что приходит в голову начинающему. На самом деле, это неплохой вариант, если в таблице совсем мало заполненных клеток и действия сводятся только к смене состояний.

void doAction(enum event e) { if (e == Press && btState == Idle) { // нажата кнопка в состоянии кнопка отпущена btState=PreClick; // переходим в состояние ожидания дребезга pressTimeStamp=millis(); // запоминаем время нажатия кнопки } if (e == Release) { // отпущена кнопка btState=Idle; // Переходим в состояние кнопка отпущена } if (e == WaitDebounce && btState == PreClick) { // Прошло время дребезга btState=Click; // считаем, что это клик } // и так далее для всех сочетаний событий и состояний }

Плюсы:

• Просто писать новичку, который впервые в руки взял ардуину.
• Первое, что приходит в голову.

Минусы:

• Сложно читать код.
• Сложно модифицировать код, если что-то поменялось в таблице.
• Ад, если большая часть клеток таблицы заполнена.

План-Б: Таблица указателей на функции

Другая крайность — это таблица переходов или функций. Я про такой подход писал в статье Обработка нажатий кнопок для Arduino. Скрестить ООП и МКА.. В двух словах, вы создаёте для каждой разной клетки таблицы отдельную функцию и делаете таблицу из указателей на них.

// определяем тип, так проще typedef void (*MKA)(enum event e); // делаем таблицу MKA action={ {&toDebounce,$toIdle,NULL,NULL,NULL,NULL}, {NULL,&toIdle,&toClick,NULL,NULL,NULL}, {NULL,&toIdle,NULL,&toHold,NULL,NULL}, {NULL,&toIdle,NULL,NULL,&toLongHold,NULL}, {NULL,&toIdle,NULL,NULL,NULL,&toVeryLongHold}, {NULL,&toIdle,NULL,NULL,NULL,NULL} }; // функция doEvent получается совсем простой void doEvent(enum event e) { if (action == NULL) return; (*(action))(e); } // Примеры функций из таблицы // В состояние «не нажата» void toIdle(enum event e) { btState=Idle; } // В состояние ожидания дребезга void toDebounce(enum event e) { btState=PreClick; pressTimeStamp=millis(); } // и так далее
Что за странные слова и значки здесь использованы?

typedef позволяет определить свой тип данных и частенько этим удобно пользоваться. Например, enum event можно определить так:

typedef enum event BottonEvent;

В программе после этого можно писать:

BottonEvent myEvent;

Я определил указатель на функцию, которая принимает один аргумент типа enum event и ничего не возвращает:

typedef void (*MKA)(enum event e);

Так я сделал новый тип данных MKA.

Значок & переводится на русский как «адрес» или «указатель». Таким образом, MKA это не значение функции, а указатель на неё.

MKA action; // Двумерный массив action переменных типа МКА

Я его сразу же заполнил указателями на функции, что выполняют действия. Если действия нет, я ставлю «указатель в никуда» NULL.

Функция doEvent проверяет указатель из таблицы в координатах «текущее состояние» x «случившееся событие» и если для этого есть указатель на функцию — вызывает её с параметром «событие».

if (action == NULL) return; // если функции нет — выходим (*(action))(e); // вызываем функцию по указателю из таблицы

Более подробно про указатели и адресную арифметику в языке C можно нагуглить в книжках типа «Язык Си для чайников».

Плюсы:

• Очень читаемый код. Не смейтесь. Достаточно один раз вкурить про массивы с указателями и вы получите простой красивый код. У вас табличка как табличка, ячейки отдельно расписаны — красота.
• Легко писать.
• Очень легко модифицировать логику.

Минусы:

• Жрёт память. Каждый указатель — это от двух до четырёх байтов. 6х6=36 клеток занимают от 72 до 144 байтов памяти и это на каждую кнопку, а если их, скажем, четыре? Напомню, у вас всего 2048 байтов памяти для популярных чипов ардуины.

Минус оказался таким жирным, что я после написания Обработка нажатий кнопок для Arduino. Скрестить ООП и МКА. и первого же применения кода в деле выпилил это всё нафиг. В итоге я пришёл к золотой середине «switch { switch {}}».

План-В: Золотая середина или switch { switch {}}

Самый распространённый, средний вариант — это использование вложенных операторов switch. На каждое событие как case оператора switch надо писать switch с текущим состоянием. Получается длинно, но более-менее понятно.

void doEvent(enum event e) { switch (e) { case Press: switch (btState) { case Idle: btState=PreClick; pressTimeStamp=millis(); break; } break; case Release: btState=Idle; break; // … так далее … } }

Умный компилятор всё-равно построит таблицу переходов, как описано в плане Б выше, но эта таблица будет в флеше, в коде и не будет занимать столь дорогую нам память переменных.

Плюсы:

• Быстрый код.
• Экономится память.
• Логика понятна. Можно читать.
• Легко менять логику.

Минусы:

• Портянка в несколько экранов при большом количестве состояний и событий, которую сложно распилить на отдельные файлы.

На самом деле, можно использовать план-В и план-А, то есть, switch по событиям, но if внутри по состояниям. На мой вкус, switch и на то и на то понятнее и удобнее, если потребуется что-то потом поменять.

Куда вставлять мой код, который зависит от нажатий кнопки?

В табличке мы не учитывали наличие других МКА сосредоточившись на нашем обработчике событий кнопки. На практике же требуется не только радоваться тому, что кнопка работает, но и выполнять другие действия.

У нас есть два важных места для вставки хорошего кода:

case Release: switch(btState) { case Click: // Вот здесь был клик и отпустили кнопку. это точно был клик. break;
case WaitDebounce: switch (st) { case PreClick: btState=Click; // Вот здесь случился клик. Кнопка может быть потом ещё нажата и будет ещё и «нажатие» итп. break;

Лучше всего, чтобы не портить красоту, написать свои функции типа offClick() и onClick(), в которых будет обрабатываться уже эти события, возможно, что они передадут его другому МКА 😀

Я обернул всю логику работы МКА кнопки в класс C++. Это удобно, так как не отвлекает от написания основного кода, все кнопки работают самостоятельно, мне не надо изобретать имена кучи переменных. Только это совсем другая история и я могу написать, как оформлять ваши МКА в классы и делать из них библиотеки для Arduino. Пишите в комментариях пожелания.

Что в итоге?

В итоге, в теории, после прочтения этой статьи должно появиться желание заменить в любимом ардуиновом скетче свой нечитаемый глючный говнокод на красивый структурированный и с использованием МКА.

Обратите внимание, что в функции loop(), которая в нашем случае лишь генерит события, нет ни одной задержки. Таким образом, после приведённого кода можно писать что-то ещё: генерить события для других МКА, выполнять ещё какой-то свой код, не содержащий delay();

Я очень надеюсь, что эта статья помогла вам понять, что такое МКА и как их реализовать в вашем скетче.

Занятие 14. Граф автомата, таблица переходов и выходов

Цель занятия. Изучение еще одного класса дискретных автоматов – автоматов с памятью, познакомится со способами описания работы этих устройств.

Теоретические положения и примеры. До сих пор мы изучали т. н. комбинационные схемы – дискретные устройства без памяти, т. е. устройства выходные сигналы которых однозначно определялись каждой комбинацией входных наборов. Теперь настала пора приступить к изучению дискретных устройств с памятью – последовательностных автоматов, т. е. устройств, реагирующих на последовательность входных наборов.

Работа последовательностного автомата определяется не только входным набором, но и собственным состоянием автомата. В свою очередь состояние Si автомата зависит от начального S0 его состояния и последовательности входных наборов, приведших его в это состояние(рис. 1).

Рисунок 58. Дискретное устройство с памятью (yi = F(x1,…,xn, Si)

Si {S0,S1,…,SL}, 2< L < m).

Мы рассматриваем дискретные устройства с конечным числом L состояний S. Рассмотрим представление автомата с памятью графом автомата. Начнем с представления триггера – автомата с 2 состояниями. Состояния представим вершинами, а связи между ними – стрелками. Стрелки снабдим условиями переходов.

Рисунок 59. D — триггер (задержка – сигнал х задерживается на один такт T).

Рисунок 60. Изображение D-триггера на схемах

Рисунок 61. С синхросигнал с периодом Т.

Сигнал D запоминается в момент, когда С=1 и хранится весь оставшийся период Т.

Теперь выполним проектирование так называемого “Секретного замка” – последовательного автомата запирающего дверь и открывающего ее, или поднимающего сигнал тревоги в зависимости от последовательностей входных воздействий.

Рисунок 62. “х1, х2”- входные переменные, “y1,y2” – выходные переменные.

1,дверь открывается,

y1=

0, дверь закрывается;

1, тревога звучит,

y2=

0, тревога не звучит.

Задана всего одна открывающая последовательность входных наборов. Еще один набор — нейтральный (х1х2 = 00), автомат остается в том же состоянии. На всех остальных последовательностях звучит сигнал тревоги.

Для нашего автомата открывающая входная последовательность пусть будет такой – х1х2= 01 11 10. Последовательности, например, начинающиеся с наборов 11 иди 10, вызовут сигнал тревоги автомата. Если дверь открыта, то она остается в этом состоянии при нейтральном входном наборе(00), любое нажатие входных кнопок вызовет закрытие двери. Наконец, если нечаянно сам владелец замка нажал неверную входную последовательность, то он может вывести автомат из тревоги, набрав единственную верную последовательность выхода из тревоги, например, х1х2 = 11 10.

Построим граф автомата “секретный замок” для уже сформулированных данных. Вначале автомат находится в некотором начальном состоянии( S0, x1x2=00, y1y2 = 00). Набираем первый набор открывающей последовательности. Автомат переходит в следующее состояние(S1, y1y2=00), но в этом состоянии автомат ждет уже второй набор открывающей последовательности. Поучив его (х1х2 =11), автомат переходит в следующее состояние(S2, y1y2 =00), в котором автомат ждет третий правильный входной набор. Получив его автомат переходит в состояние S3. Но в этом состоянии автомат, уже получив всю правильную открывающую входную последовательность, должен открыть дверь (S3, y1y2= 10). При входном нейтральном наборе (00) дверь остается открытой, после нажатия любого набора (01, или 11, или 10), дверь закрывается (S0, y1y2 =00).

Рисунок 63. Описание работы по открытию замка.

Остается реализовать режимы входа в тревогу и выхода из нее. В состоянии S1 наборы 00 и 01 уже задействованы, остаются наборы 10 и 11, при них нужно реализовать переход в тревогу — состояние (S4 y1y2 =01). В состоянии S1 нейтральный набор возвращает в то же состояние S1, наборы 01 и 10 переводят автомат в состояние тревоги S4. Аналогично в состоянии S2 нейтральный набор 00 возвращает автомат в состояние S2, наборы 11 и 01 – в состояние тревоги S4.

Рисунок 64. Описание работы по правильной последовательности и формированию сигнала тревоги.

Остается реализовать поведение автомата при выходе из тревоги. В состоянии S4 набор 11 переводит автомат в состояние S5 (y! y2 = 01). Из состояния S5 набор 10 сбрасывает тревогу (S0, y1y2 =00). При остальных наборах – возврат в состояние тревоги.

Рисунок 65. Полное описание графа автомата ”Секретный замок”.

Граф автомата полностью описывает его повеление. Но в некоторых случаях (когда число входных переменных не велико) используют другую форму задания алгоритма работы последовательностного автомата — таблица переходов и выходов автомата (ТПиВ). Таблица переходов и выходов автомата является прямоугольной матрицей, строки которой сопоставлены входным наборам и столбцы – состояниям.

Рисунок 66. Таблица переходов и выходов автомата “Секретный замок”.

Полученная таблица переходов и выходов еще представлена на так называемом абстрактном уровне. Чтобы перейти к комбинационным схемам необходимо заменить абстрактные символы состояний комбинациями наборов двоичных переменных, т. е. произвести кодирование состояний автомата. Необходимое условие правильного кодирования состояний – каждому состоянию нужно поставить свой, отличный от других состояний код. Отсюда число к внутренних переменных z1z2…zk, кодирующих состояния, вычисляется по следующей формуле k=]log2(L +1)log2(5+1), номер варианта определяется по i, младшая цифра задает открывающую последовательность, старшая — последовательность сброса тревоги. Построить таблицу переходов и выходов автомата, провести кодирование состояний и построить кодированную таблицу переходов и выходов. Построить функции z1,z2,z3,у1 и y2.

3.1.2. Синтез автомата Мили по гса. Простейшая реализация

1. Разметка состояний авто­мата Мили по ГСА.

В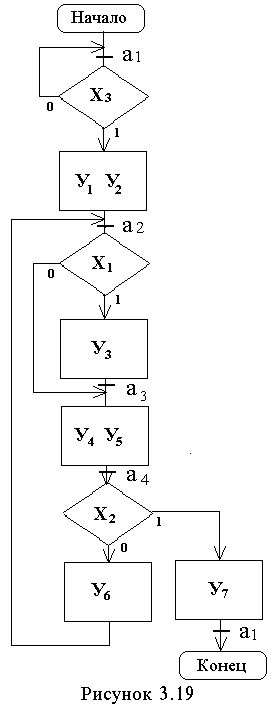отличие от автомата Мура, состояния автомата Мили не соответствуют операторным вершинам ГСА, а отмечаются на дугах ГСА перед вершинами, следующими за операторными. Исключение составляет начальное (оно же конечное) состояние автомата. Его удобно обозначать символом а0 или а1. Символом а0 или а1 отмечают вход вершины, следующей за начальной и вход конечной вершины ГСА. Входы всех остальных вершин, следующих за операторными, также отмечаются символами: а1, а2, …

Используем для примера ГСА УА (рис.3.2) для синтеза автомата Мили. Обозначим начальное состояние как а1, а остальные: а2, а3, а4.

В случае, когда в вершину, следующую за операторной, входит более чем одна дуга, состояние необходимо отметить на дуге так, что бы для всех входящих дуг соблюдалось правило разметки состояний. На ГСА (рис.3.19) это состояния а2 и а3. Состояние а2 необходимо отметить ниже входящей слева стрелки, а состояние а3 – выше входящей справа стрелки. В первом случае в а2 сошлись пути из двух операторных вершин, а во втором – путь из а2 не приводит в состояние а3 (этот переход был бы «пустым», без прохода через операторную вершину), а приводит в состояние а4 (после операторной вершины).

2.Построение графа переходов автомата Мили по ГСА.

В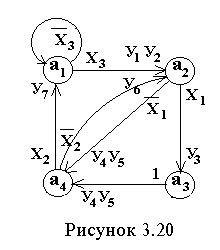ершины графа соответствуют со­стояниям автомата, дуги – переходам из со­стоянияam в состояние as. У выхода дуги из вершины графа am записываются логические условия, определяющие переход из состоя­ния am в состояние as , а у входа дуги в со­стояние as — микрокоманды, вырабатывае­мые автоматом при переходе из состояния am в состояние as (рис.3.20).

3.Построение прямой таблицы переходов автомата Мили.

Прямая таблица переходов строится по графу переходов (рис.3.20).

Таблица 3.8

№
	a 1	a 1 a 2	 x 3 x 3	y 1 y 2
	a 2	a 3 a 4	x 1  x 1	y 3 y 4 y 5
	a 3	a 4		y 4 y 5
	a 4	a 1 a 2	x 2  x 2	y 7 y 6

Количество строк в таблице равно количеству переходов в графе. В столбце аm записываются состояния, из которых начинается переход, в столбце as – состояния, в которые перешел автомат из состояния аm. В столбце Y amas записываются Yi – микрокоманды, вырабатываемые автоматом при переходе из состояния am в состояние as. В столбце Xamas записываются логические условия (их конъюнкция), обеспечивающие переход из состояния аm в состояние as.

Прямая таблица позволяет проверить полноту переходов, показанных на графе переходов: дизъюнкция всех Xama s из состояния a m должна быть равна «1» (Xamas=1). В нашем примере дизъюнкция всех Xa1as равна: Xa1as = Xa1a1  Xa1a2 =  x 3  x 3 = 1. Аналогично: Xa2as = Xa2a3  Xa2a4 = x 1  x 1 = 1, Xa3as = Xa3a4 = 1, Xa4as = Xa4a1  Xa4a2 = x2  x2 = 1.

4. Кодирование состояний автомата. Выбор элементов памяти.

Кодирование состояний автомата Мили производится также как и автомата Мура.

Используем для нашего примера минимальное кодирование состояний. Так как автомат имеет четыре состояния, то минимальное количество элементов памяти

n = ] log2 | A | log2 4 log2 4 [ = 2. В качестве элементов памяти используем 2 D-триггера: Т1 Т0 .

1. Построим обратную структурную таблицу автомата. Обратная структурная таблица автомата Мили (Таблица 3.10) содержит переходы четырех видов: am  s; m  s; m  as; am  as. Будем заполнять таблицу в указанной последовательности переходов.

2. Закодируем состояния автомата в соответствии с рекомендациями по минимальному кодированию состояний с памятью на D-триггерах:

К a 1 = 00; К a 2 = 11; К a 3 = 10; К a 4 = 01;

Таблица 3.10

6) Запишем функции выходов и управления элементами памяти сле- дующим образом. Сначала запишем функции переходов в узлы  1 и 2 :

 1 = a1 x0  a 2

 2 = a 3  a4 x4   1 x 1 x 2

Затем введем вспомогательные функции переходов f I (где i – соответствует номеру перехода вида m  as или am  as в таблице):

f 8 =  1 x 1 x 2 f 9 =  1 x 1

f 10 =  2 x 3 f 11 =  2 x 3

Далее, выразим функции D 1 и D 0 через дизъюнкцию f I :

D 1= f 8  f 9

D 0 = f 8  f 10  f 11

Функции выходов запишем аналогично с использованием функций f I , заметив, что y 5 = D 0 , а y 1 = D 1  f 10 :

y 1 = f 8  f 9  f 10 = D 1  f 10

y 2 = f 9  f 10

y 3 = f 9  f 11 .

y 4 = f 8  f 11

y 5 = f 8  f 10  f 11 = D 0

y 6 = a 4 x 4

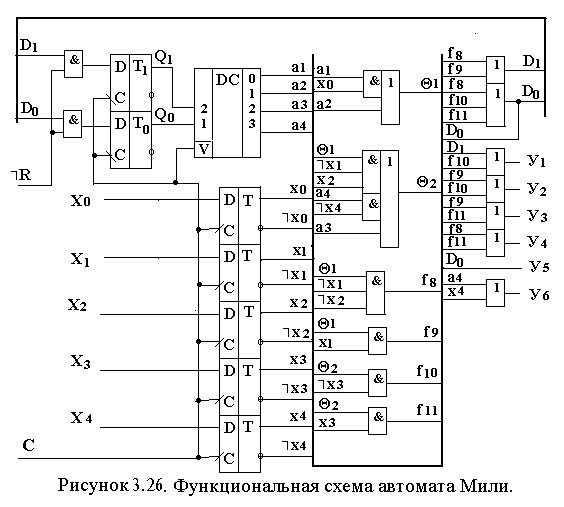
Функциональная схема автомата приведена на рис.3.26.

Рассмотрим пример построения автомата Мура с памятью состояний на RS-триггерах по ГСА рис.3.27.

В отличие от автомата Мили можно отметить еще один узел 3. В узел  3 переходы из состояний a4 и a5. Построим обратную структурную таблицу автомата Мура без учета узлов.

Обратная структурная таблица автомата Мура по ГСА (рис.3.27) без учета узлов  содержит 17 строк (17 переходов), причем в переходах участвует большое число логических условий x i . Поэтому выражения для функций управления элементами памяти Ri и Si будут достаточно громоздкими.

Обратная структурная таблица автомата Мура по ГСА (рис.3.27) без учета узлов .

Таблица 3.11

Построим обратную структурную таблицу автомата Мура с учетом узлов. При этом обратим внимание на формирование столбца таблицы Famas. Для каждого состояния as определяется множество сигналов Ri и Si, которые обеспечивают переходы из am в as, проходящие через узлы . В столбец Fama s таблицы записываются Ri и Si, которые находится объединением найденных множеств сигналов Ri и Si.

Эта операция нужна только при реализации памяти состояний автомата на RS-триггерах; в автомате на D-триггерах сигналы управления элементами памяти Di зависят только от состояния as.

Обратная структурная таблица автомата Мура по ГСА (рис.3.27) c учетом узлов  содержит 13 строк, а условия переходов значительно проще, чем без узлов.

Запишем функции выходов и управления элементами памяти следующим образом. Сначала запишем функции переходов в узлы 1, 2 и 3 :

 1 = a1 x0  a 3

 2 = a 2   1 x 1 x 2   3 x4

 3= a 4  a 5

Таблица 3.12

Затем введем вспомогательные функции переходов f I (где i – соответствует номеру перехода вида m  as или am  as в таблице):

f 9 =  3 x 4 f 10 =  1 x 1

f 11 =  1 x 1 x 2 f 12 =  2 x 3

f 13 =  2 x 3

Далее, выразим функции R I и S I через дизъюнкцию f I :

R 0 = f 12  f 9

S 0 = f 13  f 10  f 11

R 1 = f 13  f 9

S 1 = f 10  f 11  f 12

R 2 = f 12  f 13

S 2 = f 10

Функции выходов:

y 1 = a 2  a 3  a 4 y 2 = a 2  a 4

y 3 = a 2  a 5 y 4 = a 3  a 5

y 5 = a 3  a 4  a 5 y 6 = a 1

Функциональная схема автомата приведена на рис.3.28.

В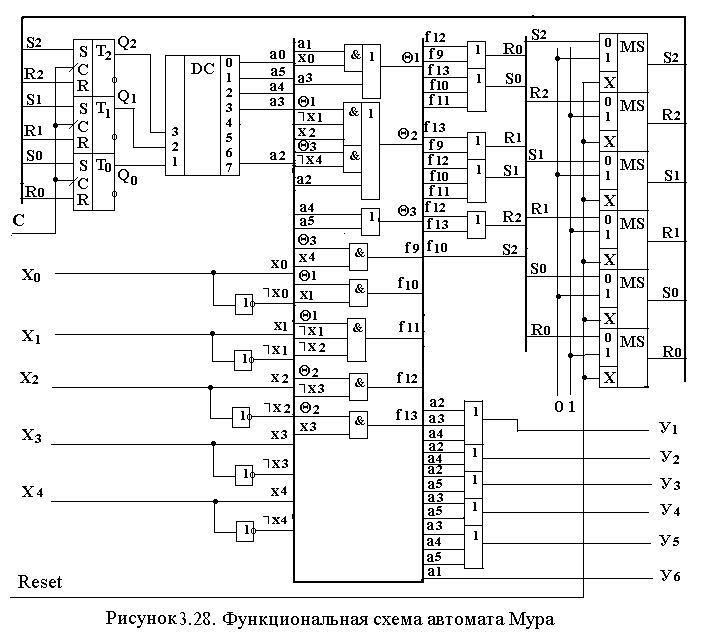приведенной схеме для установки автомата в начальное состояние используется специальная схема, состоящая из шести мультиплексоровMS. При значении Reset=0 сигналы Ri и Si, формируемые комбинационной схемой автомата, подаются через MS на соответствующие входы Ri и Si триггеров памяти состояний автомата. . При значении Reset=1 сигналы Ri и Si формируются в зависимости от схемы подключения входов «1» мультиплексоров к шинам «0» или «1». Так как в нашем примере начальное состояние a 1 имеет код Ka1=000, то на все входы Ri через MS подается «1», а на все входы S i через MS подается «0». По положительному фронту импульса синхронизации С автомат устанавливается в начальное состояние.

СИНТЕЗ АВТОМАТА МИЛИ

СИНТЕЗ МИКРОПРОГРАММНЫХ АВТОМАТОВ ПО ГРАФ-СХЕМЕ АЛГОРИТМА

Граф-схема алгоритма есть форма представления микропрограммы, которую должно выполнить операционное устройство (ОУ). При построении операционного устройства, как состоящего из операционного (ОА) и управляющего (УА) автоматов, необходимо уметь выделить функции ОА и УА из ГСА. Обычно микропрограмма представляется в виде содержательной ГСА. В этом случае для задания функций ОА необходимо перечислить все выполняемые микрооперации и все проверяемые логические условия данной микропрограммы, а также описать разрядность слов, обрабатываемых операционным устройством. На основании этих данных можно построить ОА методами, которые будут изложены в курсе «Схемотехника ЭВМ». Для инициализации выполнения той или иной микрооперации на ОА должны поступать в нужный согласно ГСА момент времени управляющие сигналы Yi. Обычно при проектировании ОУ принимают определенный способ кодирования микроопераций (чаще всего кодом, содержащим столько разрядов, сколько всего различных микроопераций) и для разработки ОА считают, что УА выдает код микроопераций, которые должны выполниться в данный момент времени.

Для УА важна последовательность выдачи соответствующих кодов микроопераций в зависимости от логических условий, вырабатываемых ОА и анализируемых УА в нужные моменты времени. Если принят способ кодирования микроопераций, то функции УА задаются кодированной ГСА. Поэтому для различных содержательных ГСА , имеющих одинаковую кодированную ГСА, ОА будут различны, но УА будет одним и тем же.

В дальнейшем будем рассматривать синтез только УА и только кодированной ГСА.

Конечный автомат, интерпретирующий микропрограмму работы дискретного устройства, называется микропрограммным автоматом. Одну и ту же ГСА можно интерпретировать как автоматом Мили, так и автоматом Мура.

Абстрактный синтез микропрограммного автомата по ГСА осуществляется в два этапа:

1. Получение отмеченной ГСА.

2. Построение графа автомата или таблиц переходов и выходов.

На этапе получения отмеченной ГСА входы вершин, следующих за операторными, отмечают символами a1, a2,.. по следующим правилам:

1) символом а1 отмечают вход вершины, следующей за начальной, а также вход конечной вершины;

2) входы всех вершин следующих за операторными, должны быть отмечены;

3) входы различных вершин, за исключением конечной, отмечаются различными символами;

4) если вход вершины отмечается, то только одним символом.

Ясно, что для проведения отметок потребуется конечное число символов а1,…,am. Результатом первого этапа является отмеченная ГСА, которая служит основой для второго этапа — перехода к графу или таблицам переходов-выходов. Пример ГСА, отмеченной для автомата Мили, представлен на рис. 55.

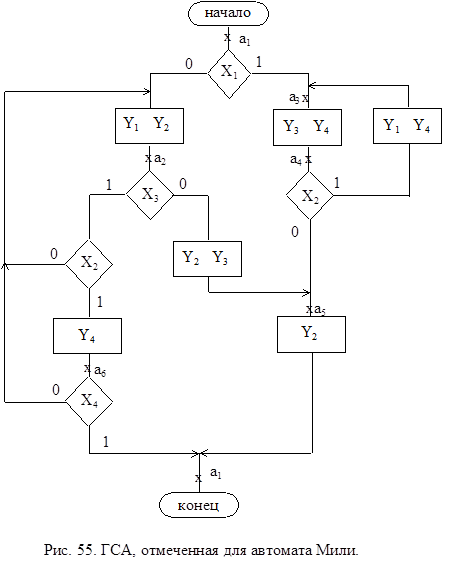
На втором этапе, из отмеченной ГСА, строят граф автомата или таблицы переходов-выходов. Для этого полагают, что в автомате будет столько состояний сколько символов ai понадобилось при отметке ГСА.

На плоскости рисунка отмечаем все состояния автомата ai. Для каждого из состояний ai определяем по отмеченной ГСА все пути, ведущие в другие состояния и проходящие обязательно только через одну операторную вершину. Например, из состояния а1(рис.55.) есть переход в состояние a2 (путь проходит через операторную вершину y1 y2) и в состояние a4 (путь проходит через вершину y3 y4). Перехода из a1 в a3 нет, так как на этом пути нет ни одной операторной вершины. Будем считать, что автомат осуществляет переход, например, из a1 в a2 при условии x1 = 0 или x1 (см.ГСА, рис.55. ) и вырабатывает на этом переходе выходные сигналы у1 у2 (то, что записано в проходимой операторной вершине ГСА, рис.55.). Значение условий х2, х3, х4 на этом переходе не оказывает влияния на автомат.

Исключение составляет только путь, ведущий в конечную вершину, он может не содержать ни одной операторной вершины (например, переход из а6 в а1), т.е. не сопровождается выработкой выходных сигналов.

Отмечаем на графе все указанные пути для всех состояний в виде дуг, которым приписываем условия перехода и выходной сигнал, вырабатываемый на этом переходе. Получим граф автомата (рис.55. ).

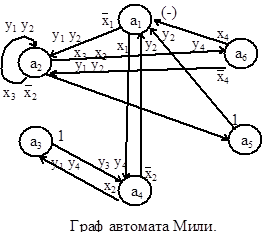
На этом графе переходам типа а3 ®a4, a5 ® a1 приписывается условие перехода 1, т.к. эти переходы являются безусловными и выполняются всегда, когда автомат попадает в состояние а3 (или а5). На основании отмеченной ГСА или графа автомата можно построить таблицу переходов-выходов. Для микропрограммных автоматов таблица переходов-выходов строится в виде списка и различаются прямая и обратная таблицы. Для данного автомата прямая таблица представлена в табл. 27., обратная — в табл. 28.

Табл. 27.Прямая таблица переходов- Табл. 28.Обратная таблица перехо-

выходов автомата Мили дов — выходов автомата Мили

В приведенных таблицах am — исходное состояние, aS — состояние перехода, Х — условие (входной сигнал), обеспечивающий переход из состояния am в состояние as, Y — выходной сигнал, вырабатываемый автоматом при переходе из am в aS.

Конечные автоматы

Лекция № 10. Праволинейные языки и конечные автоматы

Иерархия языков по Хомскому

Определение 9.4.1. Формальный язык называется языком типа 0, если он порождается некоторой грамматикой типа 0.

Определение 9.4.2. Контекстной грамматикой (контекстно-зависимой грамматикой, грамматикой типа 1) называется порождающая грамматика, каждое правило которой имеет вид hBq®haq, где BÎN, h,qÎ (NÈA)*, aÎ (NÈA)+.

Определение 9.4.3. Формальный язык называется контекстным языком, если он порождается контекстной грамматикой (грамматикой типа 1).

Определение 9.4.4. Контекстно-свободной грамматикой (бесконтекстной грамматикой, грамматикой типа 2) называется порождающая грамматика, каждое правило которой имеет вид B®a, где BÎN, aÎ(NÈA)*.

Пример 9.4.1. Пусть N={S, U, T}, A={a, b, c}, P={S®UT, U®aU, U®e, T®bTc, T®e}. Тогда G=<N, A, P, S> – контекстно-свободная грамматика, порождающая язык

L(G)={anbmcm: n³0, m³0}

Определение 9.4.5. Формальный язык называется контекстно-свободным языком, если он порождается контекстно-свободной грамматикой (грамматикой типа 2).

Определение 9.4.6. Праволинейной грамматикой (рациональной грамматикой, грамматикой типа 3) называется порождающая грамматика, каждое правило которой имеет вид B®w или B®wT, где B, TÎN, wÎA*.

Определение 9.4.7. Формальный язык называется праволинейным языком, если он порождается праволинейной грамматикой (грамматикой типа 3).

Классы формальных языков типа 0, 1, 2, 3 образуют иерархию Хомского. При этом следует иметь в виду, что:

1) каждая праволинейная грамматика является контекстно-свободной грамматикой;

2) каждая контекстно-свободная грамматика без правил вида a®e является контекстной грамматикой;

3) каждая контекстная грамматика является порождающей грамматикой типа 0.

Пример 9.4.2. Пусть N={S, H}, A={a, b}, P={S®aS, S®a, S®H, H®bH, H®b}. Тогда G=<N, A, P, S> – праволинейная грамматика, порождающая язык L(G)={anbm: n³1 или m³1}.

1. Конечные автоматы

2. Характеризация праволинейных языков

Наиболее распространенными способами конечного задания формального языка являются грамматики и автоматы. Здесь рассматриваются конечные автоматы, соответствующие в иерархии Хомского праволинейным грамматикам.

Определение 10.1.1. Конечный автомат – это пятерка

M=<Q, A, D, I, F>, где:

а) Q – конечное множество, именуемое множеством состояний, элементы которого называются состояниями и, как правило, либо нумеруются, либо просто обозначаются числами;

б) A – конечный входной алфавит (или просто алфавит);

в) D – конечное подмножество декартового произведения:

DÍ Q´A*´ Q,

причем элемент множества D вида <p, x, q> – называется переходом из состояния p в состояние q, а слово x – меткой этого перехода;

г) I – конечное множество начальных состояний (IÍ Q);

д) F – конечное множество заключительных (допускающих) состояний (FÍ Q).

Пример 10.1.1. Пусть Q={1, 2, 3, 4}, A={a, b}, I={1}, F={4}, D={<1,a,2>, <1,b,3>, <2,a,2>, <2,b,2>, <3,a,3>, <3,b,3>, <2,b,4>, <3,a,4>}. Тогда M1=<Q, A, D, I, F> – конечный автомат.

Конечные автоматы допускают описание в виде диаграмм состояний (диаграмм переходов). Каждое состояние обозначается кружком, причем начальное состояние распознается по ведущей в него короткой стрелке, а заключительное состояние отмечается двойным кружком. Переходы на диаграмме обозначаются стрелками. Стрелка из состояния p в состояние q, помеченная словом x, фиксирует наличие перехода <p, x, q>.

Например, диаграммаконечного автоматаM1 имеет следующий вид:

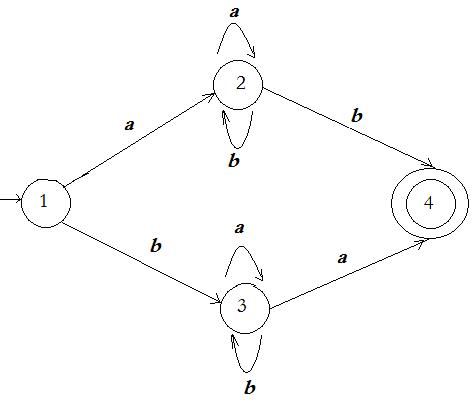
Рис. 10.1.1. Диаграмма переходов конечного автомата М1

Определение 10.1.2. Путь конечного автомата – это кортеж вида <q0, <q0, w1, q1>, q1, <q1, w2, q2>, q2…, qi-1, <qi-1, wi, qi>, qi,…qn>, где n³0 идля всех i <qi-1, wi, qi>ÎD, qiÎQ, wiÎA*. При этом:

а) q0 – начало пути; б) qn – конец пути;

в) n – длина пути; г) w1w2,…, wi, … wn – метка пути.

Путь называется успешным, если q0ÎI, а qnÎF.

Пример 10.1.2. Рассмотрим конечный автомат М1 из примера 10.1.1. Путь <1, <1, a, 2>, 2, <2, b, 2>, 2, <2, b, 4>, 4> – успешный.

Меткой этого пути будет слово abb, длина пути равна 3.

Определение 10.1.3. Слово w допускается конечным автоматом М, если оно является меткой некоторого успешного пути.

Пример 10.1.3. Рассмотрим конечный автомат М1 из примера 10.1.1. Слова abb, abbabbabb, baba, ba – допускаютсяавтоматом М1, а слова aba, abbabbaba, bab, bbb – недопускаютсяавтоматом М1.

Определение10.1.4. Множество всех слов, допускаемых конечным автоматом, называется языком, распознаваемым конечным автоматом М. Обозначается этот язык L(M). Также говорят, что автомат М распознает язык L(M).

Пример 10.1.4. Конечный автомат М1 из примера 10.1.1 распознаетязык L(M1)={awb: wÎA*}È{bwa: wÎA*} (заметим, что L(M1) – представляет собоймножествослов, у которых первая и последняя буквы не совпадают).

Пример 10.1.5. ПустьМ2=<Q, A, D, I, F>, где Q={1, 2}, I={1}, A={a, b}, F={1, 2}, D={<1, a, 2>, <2, b, 1>}. Диаграмма переходов конечного автомата М2 имеет вид:

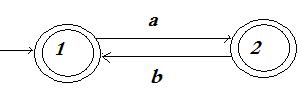
Рис. 10.1.2. Диаграмма переходов конечного автомата М2

Тогда L(M2)={(ab)n: n³0}È{(ab)na: n³0 }.

Определение 10.1.5. Два конечных автомата эквивалентны, если они распознают один и тот же язык.

Пример 10.1.6. Конечныеавтоматы, представленные следующими диаграммами (рис. 10.1.3), эквивалентны.

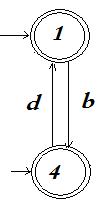Рис. 10.1.3. Диаграммы переходов эквивалентных конечных автоматов

Определение 10.1.6. Язык L называется автоматным, еслисуществует конечный автомат, распознающий этот язык.

Определение 10.1.7. Состояние q достижимо изсостояния p, если существует путь, началом которого является p, а концом – q.

Теорема 10.1.1. Каждый автоматный язык распознается некоторым конечным автоматом, в котором каждое состояние достижимо из некоторого начального состояния и из каждого состояния достижимо хотя бы одно заключительное состояние.

Иными словами, каждый конечный автомат может быть преобразован в эквивалентный автомат, в котором каждое состояние достижимо из некоторого начального состояния и из каждого состояния достижимо хотя бы одно заключительное состояние. Пример подобного преобразования приведен на рис. 10.1.3.

Теорема 10.1.2. Каждый автоматный язык распознается некоторым конечным автоматом, не содержащим переходов с метками длины больше единицы и имеющим ровно одно начальное состояние и ровно одно заключительное состояние.

Теорема 10.1.3. Каждый автоматный язык распознается некоторым конечным автоматом, содержащим только переходы с метками длины единица и имеющим ровно одно начальное состояние.

Определение 10.1.8. Конечныйавтомат M=<Q, A, D, I, F> называется детерминированным, если:

1) множество начальных состояний I содержит ровно один элемент;

2) длина метки каждого перехода равна единице;

3) для любого символа aÎA и для любого состояния pÎQ существует не более одного состояния qÎQ со свойством <p, a, q>ÎD.

Примером детерминированного конечного автомата может служить автомат М2 из примера 10.1.5. Примером недетерминированного конечного автомата может служить автомат М1 из примера 10.1.1.

Определение 10.1.9. Детерминированный конечныйавтомат M=<Q, A, D, I, F> называется полным, если для каждого состояния pÎQ и для любого символа aÎA найдется такое состояние qÎQ, что<p, a, q>ÎD.

Теорема 10.1.4. Каждый автоматный язык распознается некоторым полным детерминированным конечным автоматом.

Иными словами, каждому конечному автомату можно сопоставить эквивалентный ему полный детерминированный конечный автомат.

Пример 10.1.7. Диаграмма полного детерминированного конечного автомата, эквивалентного автомату М1 из примера 10.1.1, выглядит следующим образом:

Рис. 10.1.4. Диаграмма полного детерминированного конечного автомата,

эквивалентного автомату М1

Пример 10.1.8. Диаграмма полного детерминированного конечного автомата, эквивалентного автомату М2 из примера 10.1.5, выглядит следующим образом:

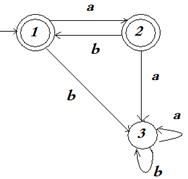
Рис. 10.1.5. Диаграмма полного детерминированного конечного автомата,

эквивалентного автомату М2

3.3.6.2. Пример автомата Мили

В отличие от автомата Мура, который имеет выходы, определяемые только настоящим состоянием автомата, в автомате Мили выходы определяются как состоянием автомата, так и входами схемы. Это делает выходы автомата Мили не полностью синхронными с сигналом синхронизации схемы. В графе автомата Мили выходы записываются вдоль ребер, которые выходят из состояний автомата.

Рис. 3.68. Детектор последовательности 101 типа Мили

На рис. 3.68 показана диаграмма состояний детектора последовательности 101 типа Мили. Автомат имеет три состояния: reset, got1 и got10. Когда автомат находится в состоянии got10, если вход х принимает значение 1, то автомат со следующим импульсом синхросигнала готовится перейти в следующее состояние. В то время как ожидается импульс синхросигнала, его выход принимает значение 1. В то время как это случается, если появляется импульс синхросигнала, автомат выходит из состояния got10 и переходит в состояние got1. Этот автомат позволяет перекрывать последовательности бит. Автомат не имеет внешнего сбрасывающего механизма. Последовательность двух нулей на входе х переводит автомат в состояние reset максимум за два импульса синхросигнала.

Описание на языке Verilog детектора последовательности 101 типа Мили показано на рис. 3.69. После объявления входов и выходов декларация parameter определяет битные шаблоны (коды) для состояний автомата. Заметим, что здесь не используется код состояний 3 или 2 Ъ11. Как и в предыдущем примере, для хранения настоящего состояния автомата мы используем двухбитную переменную current типа reg.

После объявлений блок initial устанавливает начальное состояние автомата в reset. Эта процедура для инициализации автомата годится только для моделирования, поскольку она не является синтезируемой.

Рис. 3.69. Описание на языке Verilog детектора последовательности 101 типа Мили

Этот пример использует блок always для определения переходов между состояниями и отдельный оператор assign для установки значений выхода z. Оператор always, ответственный за переходы между состояниями, является чувствительным к сигналу синхронизации схемы и имеет оператор case, который включает альтернативы для каждого состояния автомата. Рассмотрим, например, состояние got10 и соответствующий ему фрагмент описания на языке Verilog, показанный на рис. 3.70. Описание языка Verilog этого состояния определяет следующее состояние автомата. Заметим, что в этом фрагменте описания показанная альтернатива оператора case не имеет операторных скобок begin и end. Действительно, ключевые слова begin и end не появляются в блоках, следующих за каждым из ключевых слов if и else.

Язык Verilog требует операторных скобок begin и end только в том случае, если в блоке имеется более чем один оператор. Использование операторных скобок для одного оператора является необязательным. Поскольку каждая из частей if и else содержит только один оператор, то ключевые слова begin и end не используются. Кроме того, поскольку весь оператор if-else сокращается до одного оператора, то для case-альтернативы также удаляются ключевые слова begin и end.

Последняя case-альтернатива, показанная на рис. 3.69, является альтернативой default. Когда проверка переменной current для всех альтернатив до оператора default является неудачной, принимается эта альтернатива. Имеется несколько причин, по которым мы используем эту умалчиваемую альтернативу. Одна из них состоит в том, что автомат использует только три из возможных четырех 2-битных кода состояний, а код 2 Ъ11 не используется. Если автомат всегда начинает свою работу в этом состоянии, то выбор по умолчанию сделает reset следующим состоянием автомата. Другая причина, по которой мы используем default, состоит в том, что язык Verilog допускает четырехзначную логическую систему, которая включает значения Z и X. Если переменная current когда-либо примет значение Z или X и не подойдет ни одна из case-альтернатив, то принимается альтернатива по умолчанию. Следующая причина для использования default состоит в том, что данный автомат не имеет аппаратного сброса, поэтому таким способом обеспечиваем перевод автомата в состояние reset. Последняя причина в использовании default состоит в том, что хорошей идеей является возможность иметь такую альтернативу.

Рис. 3.70. Кодирование состояния автомата Мили

Последний оператор во фрагменте описания на рис. 3.70 является оператором assign, который устанавливает значение выхода схемы г. Этот оператор является параллельным оператором, и он не зависит от записанного выше оператора always. Когда переменные current или х изменяются, вычисляется правая часть оператора assign, и значение 0 или 1 присваивается выходу z. Условие в правой части этого оператора присваивания соответствует значениям, передаваемым на выход г в графе автомата на рис. 3.68. В частности, выход принимает значение 1, когда переменная current имеет значение dot10 и х равен 1, в противном случае выход равен 0. Этот оператор реализует структуру комбинационной схемы с входами current и х и выходом г.

Кодируем автомат, ставя в соответствие каждому символичес­кому сигналу произвольный двоичный код (число разрядов кода со­ответствует найденным r, n, m).

Таблица 4 – Кодировка автомата Мили

Входные сигналы

Выходные сигналы

Сигналы памяти

Состояние входа

Биты кода

Состояние выхода

Биты кода

Внутренние состояние

Биты кода

С учетом введенных кодов переводим таблицы переходов и выходов в двоичный алфавит (рис.7).

Рисунок 7. Двоично-кодированные таблицы КА Мили

4. По таблице выходов λ составляем логические уравнения для выходных сигналов у1 и у2. Учтем, что в каждой клетке таблицы левый бит характеризует сигнал у1, правый — у2. Записывая уравнения «по единицам», получаем СДНФ:

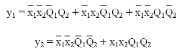
5. Преобразуем таблицу переходов автомата в таблицу возбуждения памяти. Для обеспечения каждого отдельного перехода из исходного состояния памяти в последующее нужно подать на входы элемен­тов памяти (синхронных триггеров) определенные сигналы. Именно эти сигналы и заносятся в соответствующие клетки таблицы возбуждения памяти.

На рис.8 для примера рассмотрены возможные переходы в первом столбце таблицы переходов (состояния входов х1х2 на данном этапе несущест­венны) :

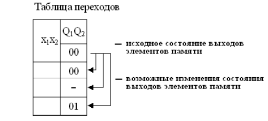
Рисунок 8. Пример переходов КА Мили

Выделим первое возможное изменение состояния Q1Q2: 00→00. По­скольку каждый бит характеризует состояние выхода отдельного JK-триггера, то согласно таблице возбуждения такого триггера для перевода его выхода из состояния 0 в состояние 0 (т.е. сохранение состояния) необходимо подать на вход J сигнал 0, а на вход К — все равно нуль или единицу. Безразличное состояние входа изображается прочерком в таблице возбуждения памяти. Это иллюстрируется рис. 9 :

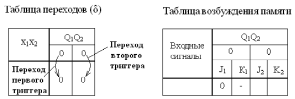
Рисунок 9. Заполнение таблицы возбуждения памяти

Ясно, что переход второго триггера должен быть отображен аналогичной комбинацией его входных сигналов (на рисунке не показано).

При переходе памяти в следующее возможное состояние процесс показан на рис.10 :

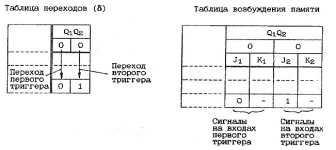
Рисунок 10. Переход памяти в следующее состояние

Окончательный вид таблицы возбуждения памяти автомата после рассмотрения переходов по всем столбцам приведен в таблице 5.

Таблица 5 – Таблица возбуждения памяти, выполненной на JK- триггерах

Х1 Х2	Q1 Q2
	J1 K1	J2 К2	J1 K1	J2 К2	J1 K1	J2 К2	J1 K1	J2 К2
							—	—
	—	—					—	—
			—	—

Если в качестве элементов памяти использовать Т-триггеры, то таблица возбуждения памяти будет иметь более простой вид, так как Т-триггер имеет один информационный вход (таблица 6).

Таблица 6 – Таблица возбуждения памяти, выполненной на Т- триггерах

Х1Х2

В случае использования D-триггеров таблица возбуждения памяти повторяет таблицу переходов.

6. По таблице возбуждения памяти (для JK-триггеров) составляем логические уравнения сигналов на каждом информационном входе каж­дого триггера. Записывая их «по единицам”, получаем следующие СДНФ:

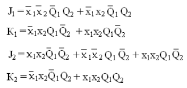
7. Минимизируем уравнения, полученные в пп.4 и 6, при помощи карт Карно. Так как функции переходов и выходов не определены на некоторых наборах аргументов, доопределяем карты Карно на этих на­борах единицами или нулями с целью проведения контуров наиболее высокого ран­га (положение этих единиц отмечено на картах символом *). Так, для y1 и y2 карты Карно имеют вид рис. 11:

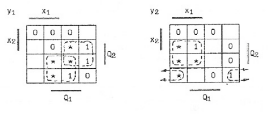
Рисунок 11. Карты Карно для выходных сигналов

Записываем минимальные ДНФ:

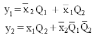
Проводя минимизацию остальных функций, получаем следующие функции:

8. По полученным минимальным формам составляем логическую схе­му автомата на микросхемах выбранной серии. Этот процесс сложности не представляет, поэтому приведем только функциональную схему автомата Мили (рис.12).

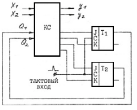
Рисунок 12. Функциональная схема КА Мили