Задача о ферзях

Автор вПрограммы

Глава 8. Задача о восьми ферзях

Задача о восьми ферзях, как и задача о ходе коня, является одной из самых знаменитых математических задач на шахматной доске. Если задачей о коне занимался Леонард Эйлер, то задача о ферзях привлекла внимание другого великого математика — Карла Гаусса.

Сколькими способами можно расставить на шахматной доске восемь ферзей так, чтобы они не угрожали друг другу, т. е. никакие два не стояли на одной вертикали, горизонтали и диагонали?

Найти ту или иную расстановку ферзей, удовлетворяющую условию задачи, не так трудно (четыре решения приведены на рис. 43). Значительно труднее подсчитать общее число существующих расстановок; собственно, в этом и состоит задача о восьми ферзях. Ясно, что как и в случае ладей, больше восьми не атакующих друг друга ферзей на шахматной доске расставить невозможно. И, соответственно, на доске n×n необходимым образом нельзя расставить более n ферзей (в общем виде задача будет рассмотрена несколько ниже).

♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕
♕

Рис. 43. Восемь ферзей, не угрожающих двуг другу на шахматной доске

Любопытно, что многие авторы ошибочно приписывают задачу о восьми ферзях и ее решение самому Гауссу. На самом деле первым ее сформулировал в 1848 г. немецкий шахматист М. Беццель. Доктор Ф. Наук (слепой от рождения) нашел 60 решений и опубликовал их в газете «Illustrierte Zeitung» от 1 июня 1850 г. Лишь после этого Гаусс увлекся задачей и нашел 72 решения, которые сообщил в письме к своему другу астроному Шумахеру от 2 сентября 1850 г. Полный же набор решений, состоящий из 92 позиций, получил все тот же Ф. Наук (он привел их в упомянутой газете от 21 сентября 1850 г.). Эта хронология установлена известным немецким исследователем математических развлечений В. Аренсом, который в своих книгах немало места уделил рассматриваемой задаче.

Доказательство того, что 92 решения исчерпывают все возможности, было получено лишь в 1874 г. английским математиком Д. Глэшером (при помощи теории определителей).

В принципе, расставляя на доске восемь ферзей всевозможными способами, мы в конце концов найдем все устраивающие нас расстановки. Однако этот путь чересчур долог и скучен. Можно ограничиться только решениями соответствующей задачи о ладьях и отобрать среди них такие, в которых никакая пара ладей не стоит па одной диагонали. Но и в этом случае перебор довольно велик (понадобятся, как мы знаем, более 40000 попыток). Таким образом, при решении задачи «вручную» (а именно так поступали в прошлом веке) вынужденный перебор расстановок должен быть хорошо продуман. Известно много способов организовать более или менее разумный поиск искомых расположений ферзей (методы Пермантье, Ла-Ное, Гюнтера, Глэшера, Лакьера и др.). Эти способы описаны в многочисленной литературе по занимательной математике (в основном в прошлом столетии и начале нынешнего). В наш век вычислительных машин задача такого сорта не смогла бы вызвать столь живой интерес. Ведь достаточно составить несложную программу для ЭВМ — и уже через несколько минут после ее введения в машину все 92 необходимые позиции будут выданы на печать.

Из каждого решения задачи о ферзях можно получить ряд других при помощи поворотов (вращений) доски вокруг центра на 90, 180 и 270° по часовой стрелке (поворот на 360° приводит к исходной позиции). Из данной расстановки ферзей новую можно получить также зеркальным отражением доски относительно одной из пунктирных прямых на рис. 43 (1-я позиция)35. Например, из первой расстановки на этом рисунке при повороте доски на 90° мы получаем третью, а при отражении относительно линии, разделяющей королевский и ферзевый фланги, — четвертую. При помощи других поворотов и отражений можно получить еще пять решений.

Итак, при поворотах и отражениях доски из одной расстановки ферзей получаются, вообще говоря, семь новых. Доказано, что в общем случае на доске n×n (при n > 1) для любой расстановки n ферзей, не угрожающих друг другу, возможны лишь три ситуации: а) при одном отражении доски получается новая расстановка, а повороты и другие отражения ничего нового не дают; б) новое решение получается при повороте доски на 90°, а отражения дают еще две расстановки; в) все три поворота и четыре отражения доски приводят к восьми несовпадающим расстановкам (включая исходную).

В случае а) исходное решение называется дважды симметрическим, в случае б) — симметрическим, а в случае в) — простым. Для обычной доски каждое решение является либо простым, либо симметрическим, а дважды симметрических не существует. Алгебраическую интерпретацию решений каждого класса можно найти у Окунева.

Множество (набор) расстановок восьми ферзей называется основным,если они, во-первых, не переходят друг в друга при поворотах и отражениях доски, и, во-вторых, любая другая расстановка получается из какой-нибудь основной при помощи этих преобразований. Известно, что всякий набор основных решений задачи содержит ровно 12 позиций (расстановок восьми ферзей). Приведем одип из таких наборов:

Остальные 80 позиций получаются из этих двенадцати в результате поворотов и отражений доски. Первые 11 расстановок являются простыми, и лишь последняя — симметрической. Таким образом, всего на доске существует 11×8 + 1×4 = 92 расстановки восьми ферзей, не угрожающих друг другу.

Рассматривая основные расстановки, можно обнаружить те или иные интересные особенности их. Например, легко заметить внешнюю симметрию последней расстановки (2-я позиция на рис. 43). Это основное решение, единственное в своем роде, характеризуется также тем, что только у него центральная часть доски (квадрат 4×4) свободна от ферзей. Еще одно его свойство состоит в том, что ферзями не занята главная диагональ доски a1 — h8 (этим свойством обладает и первое основное решение).

Первая расстановка на рис. 43 любопытна тем, что здесь никакие три ферзя не стоят на одной прямой, проведенной через центры полей (имеются в виду не только вертикали, горизонтали и диагонали доски* но и прямые с другими углами наклона).

Всякое решение задачи можно записать, как набор (t1, t2, … t8), представляющий собой перестановку чисел 1, 2, …, 8. Здесь ti — номер горизонтали, на которой стоит ферзь i-й вертикали. Так как никакие два ферзя не находятся на одной горизонтали, то все tx различны, а поскольку ферзи не стоят и на одной диагонали, то для любых i, j (i < j ≤ 8) имеем: |tj — ti| ≠ j — i.

Числовая запись расстановок ферзей иногда бывает очень удобной. Например, для нахождения расстановок при фиксированном расположении ферзя на a1 достаточно из всех 92 позиций, записанных в числовой форме, отобрать такие, у которых первая координата равна 1. Если фиксировано положение ферзя на d3, то следует выделить позиции, у которых на четвертом месте стоит число 3, и т. д.

Запишем числа 1, 2, …, 8 сначала по возрастанию, а потом по убыванию. После этого сложим числа каждой из этих двух перестановок с числами произвольной перестановки, например (3, 7, 2, 8, 5, 1, 4, 6):

+ 1, 2, 3, 4, 5, 6, 7, 8 + 8, 7, 6, 5, 4, 3, 2, 1
3, 7, 2, 8, 5, 1, 4, 6 3, 7, 2, 8, 5, 1, 4, 6
4, 9, 5, 12, 10, 7, 11, 14 11, 14, 8, 13, 9, 4, 6, 7

Полученные суммы образуют два набора чисел: (4, 9, 5, 12, 10, 7, 11, 14) и (11, 14, 8, 13, 9, 4, 6, 7). Возникает следующая задача.

Какие перестановки чисел 1, 2,…, 8 дают в результате указанной операции сложения два таких набора, в каждом из которых все числа различны?

Задача о восьми ферзях заинтересовала Гаусса именно в связи с этой чисто арифметической задачей. Оказывается, между решениями задачи о ферзях и решениями описанной арифметической задачи существует взаимно однозначное соответствие. Другими словами, каждая расстановка восьми ферзей, не угрожающих друг другу, дает решение арифметической задачи — и наоборот. Для выбранной перестановки оба набора состоят из различных чисел, и это не случайно — она соответствует первой позиции на рис. 43.

Нетрудно видеть, что при поворотах n отражениях доски одни решения получаются из других при помощи простых арифметических операций над координатами полей, занятых ферзями. Исследование этих операций позволяет обнаружить дополнительные свойства решений (некоторые из которых приведены у Окунева).

Задача о n ферзях. На шахматной доске n×n расставить n ферзей так, чтобы они не угрожали друг другу.

На доске 1×1 один ферзь ставится на единственное поле, и решение существует. На доске 2×2 один ферзь, где бы он ни стоял, угрожает всем полям доски, и второго ферзя поставить некуда. При любой расстановке трех ферзей на доске 3×3 хотя бы два из них угрожают друг другу. Итак, при n, равном 2 или 3, задача не имеет решений.

Что касается случаев n > 3, то известно, что на любой доске n×n можно расставить n ферзей так. чтобы они не угрожали друг другу. Доказательству этого далеко не очевидного факта посвящено много статей, в том числе в серьезных математических изданиях.

На доске 4×4 существует единственная основная расстановка, причем дважды симметрическая (a2, b4, c1, d3), т. е. всего здесь имеется два решения. На доске 5×5 основных расстановок две: 1) a2, b4, c1, d3, e5; 2) a2, b5, c3, d1, e4; всего же имеется десять искомых позиций. Интересно, что из них можно выбрать пять таких, при наложении которых друг на друга 25 ферзей заполнят все поля доски 5×5. Аналогичное наложение в общем случае возможно только при тех и, которые не делятся ни на 2, ни на 3. Из этого, в частности, следует, что для обычной доски подобрать восемь решепий, для которых ферзи заполняют всю доску, невозможно.

Обобщая указанное выше алгебраическое свойство решений задачи о восьми ферзях, получаем, что расстановка (t1, t2, … tn) n ферзей на доске n×n является искомой, если для любых i, j (i < j < n): |tj — ti| ≠ j — i. Здесь по-прежнему ti — номер горизонтали, на которой стоит ферзь i-й вертикали, а набор t1, …, tn есть перестановка чисел 1, …, п. Таким образом, для решения задачи в общем случае достаточно найти перестановку чисел 1, …, n, удовлетворяющую указанному условию.

Сейчас мы опишем одну возможную схему искомого расположения n ферзей на доске n×n при всех n > 5. Доказательство того, что в полученных расстановках наше условие выполняется, можно найти, например, у Окунева или у Ягломов.

Рассмотрим последовательно ряд случаев. Пусть сначала n четно, причем n = 6k или n = 6k + 4. Половину всех ферзей поставим на первых n/2 вертикалях ходом коня, начиная со второй горизонтали и передвигаясь каждый раз на 2 поля вверх и на 1 вправо. Вторую половину поставим на оставшихся n/2 вертикалях тем же способом, но начиная с первой горизонтали. Для доски 6×6 (n = 6k, k = 1) это дает такую расстановку ферзей: a2, b4, c6, d1, e3, f5 (решение, представленное на рис. 45 для n = 10, получается иным образом).

При n = 6k + 2 предыдущий прием уже не проходит, и ферзей приходится расставлять более «хитрым» способом. Расположим их ходом коня со второй вертикали по

(n/2 — 2)-ю, начиная с третьей горизонтали, и далее с

(n/2 + 3)-й вертикали по (n — 1)-ю, начиная с шестой горизонтали. В результате свободными останутся шесть вертикалей и шесть горизонталей доски, на которых шесть ферзей должны занять поля с такими координатами: (1, n — 3), (n/2 — 1, 1); (n/2, n — 1), (n/2 + 1, 2), (n/2 + 2, n), (n, 4). При n = 14 (n = 6k + 2, k = 2) получаем расстановку на рис. 44. Кстати, на обычной доске 8×8 (8 = 6k + 2, к = 1) расстановка восьми ферзей указанным способом совпадает все с тем же замечательным решением на рис. 43 (2-я позиция), но заметить закономерность расположения ферзей здесь вряд ли возможно.

Нам осталось рассмотреть задачу для нечетных значений n. Чтобы получить решение в этом случае, достаточно заметить, что в предложенных нами расстановках на «четных» досках главная диагональ (идущая из левого нижнего угла в правый верхний) оставалась свободной. Учитывая это обстоятельство, искомую расстановку n ферзей на доске n×n (при нечетном n) можно получить следующим образом. На вертикалях и горизонталях этой доски с номерами от 1 до (n — 1) расставим (n — 1) ферзя так, как это делается на доске (n — 1)×(n — 1) (n — 1 четно!), а затем n-то ферзя расположим в правом верхнем углу доски. Описанным способом можно получить первую расстановку ферзей на доске 5×5 из указанной расстановки на доске 4×4, а из расстановки ферзей на доске 6×6 имеем следующую для n = 7: a2, b4, c6, d1, e3, f5, g7.

♕
♕
♕
♕
♕
♕
♕
♕
♕
♕

Рис. 45. Десять ферзей-магарадж, не угрожающих друг другу на доске 10×10

Таблица 1
n 1 2 3 4 5 6 7 8 9 10 11 12
Число решений 1 — — 2 10 4 40 92 352 724 2680 14200

В табл. 1 указано общее число решений задачи об n ферзях для досок n×n при n от 1 до 12. Нахождение общей формулы для числа расстановок n ферзей, не угрожающих друг другу на доске n×n, представляет собой весьма сложную проблему.

Ферзь, как мы знаем, сочетает в себе ходы ладьи и слона. Фигуру, которая ходит одновременно как ладья, слон и конь, шахматвые композиторы называют магараджей или амазонкой. Как обстоит дело с расстановкой на доске 8×8 восьми таких сверхферзей?

Оказывается, что восемь магарадж, не атакующих друг друга, расставить на доске 8×8 невозможно. Проанализировав все 12 приведенных выше основных расстановок, мы легко убедимся, что всякий раз по меньшей мере три пары ферзей связаны между собой ходом коня. На доске 9×9 девять наших мощных фигур также не могут находиться в безопасности. И лишь на доске 10×10 можно расставить десять «мирных» магарадж. При этом имеется всего одно основное решение, показанное на рис. 45, где ферзи играют роль магарадж.

Склеивая друг с другом вертикальные или горизонтальные края доски, мы получаем цилиндрическую шахматную доску. Ниже мы еще вернемся к цилиндрическим шахматам, а сейчас рассмотрим одну «цихиндрическую» задачу, естественно обобщающую задачу о восьми ферзях.

Можно ли на цилиндрической шахматной доске расставить восемь ферзей так, чтобы они не угрожали друг другу?

Оказывается, что если на обычной доске имеется 92 искомые расстановки, то на цилиндрической уже нет ни одной! Докажем это, считая, что такая доска получается в результате склеивания вертикальных краев (см. рис. 68,а).

187 286 385 484 583 682 781 888
178 277 376 475 574 673 772 871
161 268 367 466 565 664 763 862
152 251 358 457 556 655 754 853
143 242 341 448 547 646 745 844
134 233 332 431 538 637 736 835
125 224 323 422 521 628 727 826
116 215 314 ♕413 512 611 718 817

Рис. 46. Задача о восьми ферзях на цилиндрической доске

Возьмем обычную шахматную доску, помня о том, что ее края склеены. Это означает, в частности, что ферзь с d1 может пойти на a4 и далее, не останавливаясь, через b5 на e8 (этот путь показан стрелкой на рис. 46), и, значит, поля d1 — a4 и b5 — e8 составляют одну диагональ. Запишем на каждом поле доски три цифры, совпадающие, соответственно, с номерами вертикали, горизонтали и диагонали, проходящих через это поле. Рассматриваются диагонали, параллельные стрелкам на рис. 46, здесь же показана выбранная нами нумерация диагоналей.

Если восемь ферзей не угрожают друг другу, то на восьми полях, занимаемых ими, все первые цифры различны и, значит, образуют полный набор чисел 1, 2, …, 8. То же утверждение справедливо для вторых и для третьих цифр. Итак, сумма всех 24 цифр, стоящих на полях с ферзями, равна (1 + … + 8)×3 = 108. Так как сумма цифр каждого поля делится на 8, то и найденная сумма должна делиться на 8, однако 108 на 8 не делится — противоречие!

35. Конечно, при поворотах n отражениях доски всегда предполагается, что система координат фиксирована. В противном случае при любых операциях с доской мы бы имели одно и то же решение.

Разбираемся, что же там нового открыли в задаче о ферзях

Пару месяцев назад появилась занятная статья с анализом классической задачи о расстановке ферзей на шахматной доске (см. детали и историю ниже). Задача невероятно известная и вся уже рассмотрена под микроскопом, поэтому было удивительно, что появилось что-то действительно новое.


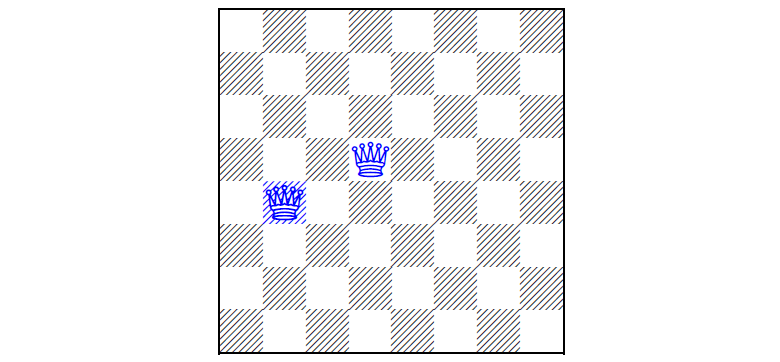
Сможете поставить ещё шесть? А найти все решения?
(картинка из статьи)

Далее, к сожалению, произошла какая-то совершенно невразумительная история из цепочки вот таких вот превращений:

  • Отличная статья —пресс служба университета—> невразумительный пресс-релиз.
  • Пресс релиз —занятный перевод—> непонятная статья на гиктаймс

Стоит отметить, что пять наугад открытых ссылок на русском ещё меньше проясняли картину происходящего.

Я тут подумал — надо бы кому-то эту странную цепочку прервать и нормальным языком изложить суть событий.

О чём пойдёт речь:

  • История задачи
    • Латинский квадрат
    • Задача о восьми ферзях
  • Три типа задачи «о ферзях»
    • Расстановка N ферзей
    • Подсчет числа решений
    • Дополнение до N ферзей
    • Вариации задачи
  • Модели и сложность
    • Линейный поиск для N ферзей
    • Как считать число решений на практике
    • Дополнение до N
  • Выводы

    Три типа задачи «о ферзях»

    Есть три наиболее популярных постановки задачи о ферзях

    Расстановка N ферзей

    Задача формулируется очень прямолинейно.

    Дано: пустая доска NxN, например 8х8

    (в принципе понятно, что достаточно просто указать N, но так наглядней)

    Найти: расстановку максимально возможного числа ферзей

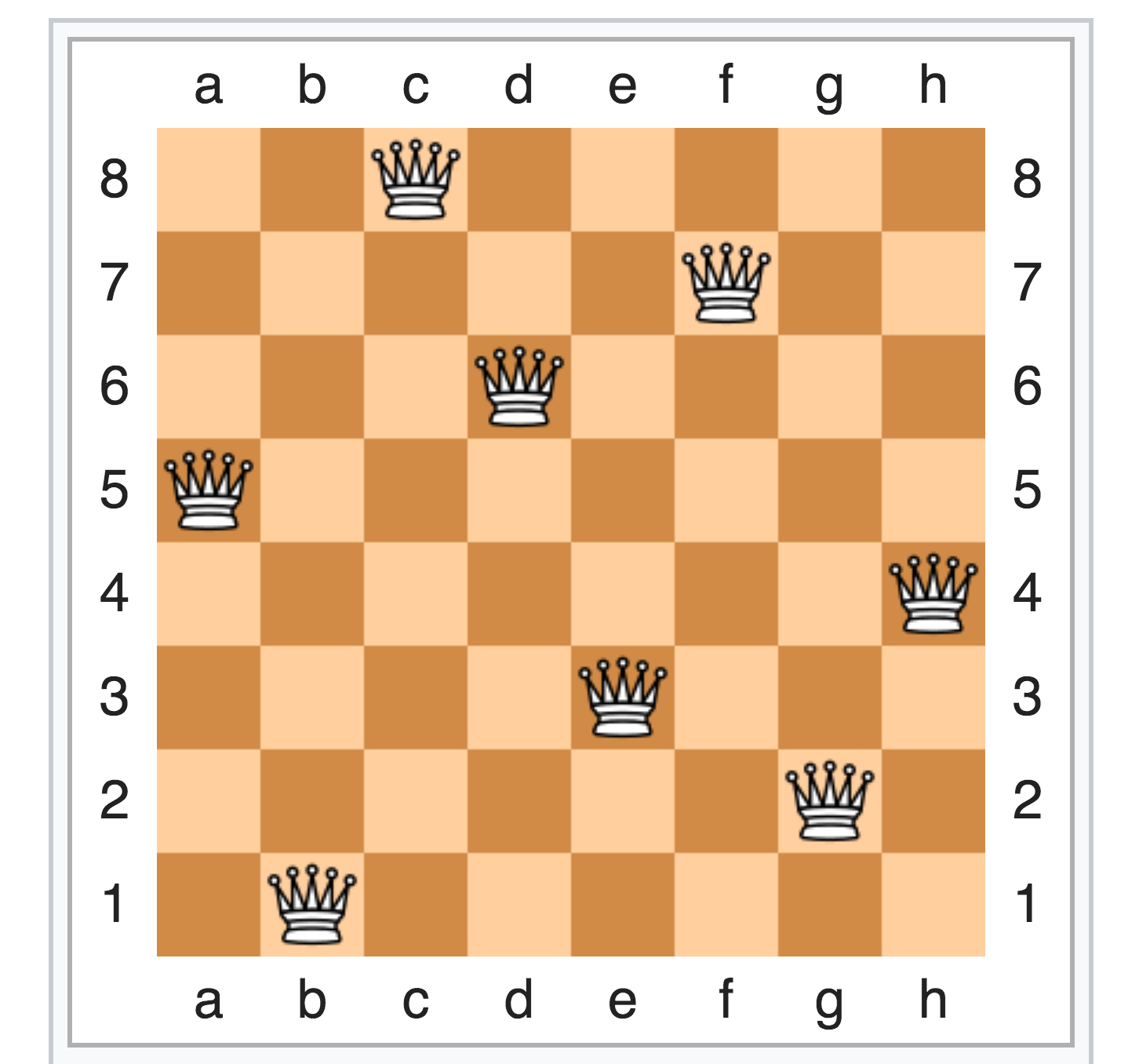
    Т.е. на вход число — размер доски, а на выход позиции ферзей (одного решения).

    Подсчет числа решений

    Задача ставится тоже достаточно просто:

    Дано: размер пустой доски N
    Найти: H число возможных расстановок N ферзей на доске

    Например, размер доски N = 1, тогда число возможных расстановок H = 1.
    N = 8 => H = 92.

    Дополнение до N ферзей

    Вот тут формулировка чуть-чуть коварней:

    Дано: размер доски N и M позиций уже установленных ферзей
    Найти: позиции оставшихся N — M ферзей

    Визуально все как на КПДВ:

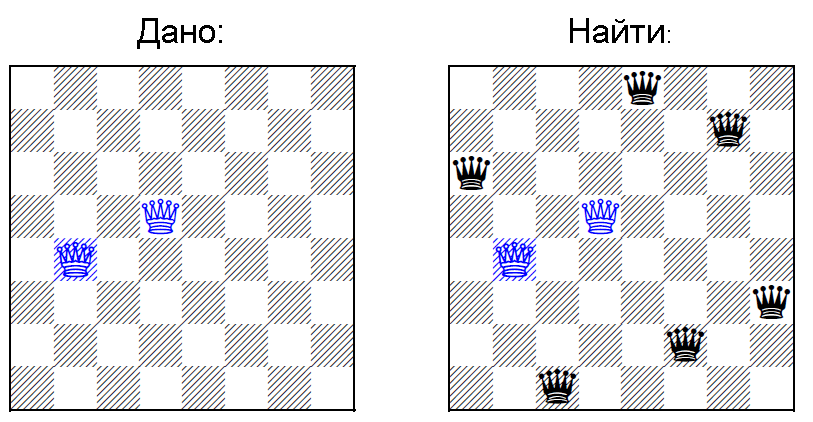
    (картинка также из оригинальной статьи)

    Вариации задачи

    Вообще говоря, вариаций задачи больше: см. например: расстановку белых и черных ферзей
    http://www.csplib.org/Problems/prob110
    однако здесь мы рассматриваем только основной классический вариант.

    В подобной вариации решения существенно отличаются (белые не бьют белых, а черные черных: в случае путаницы — см. ):

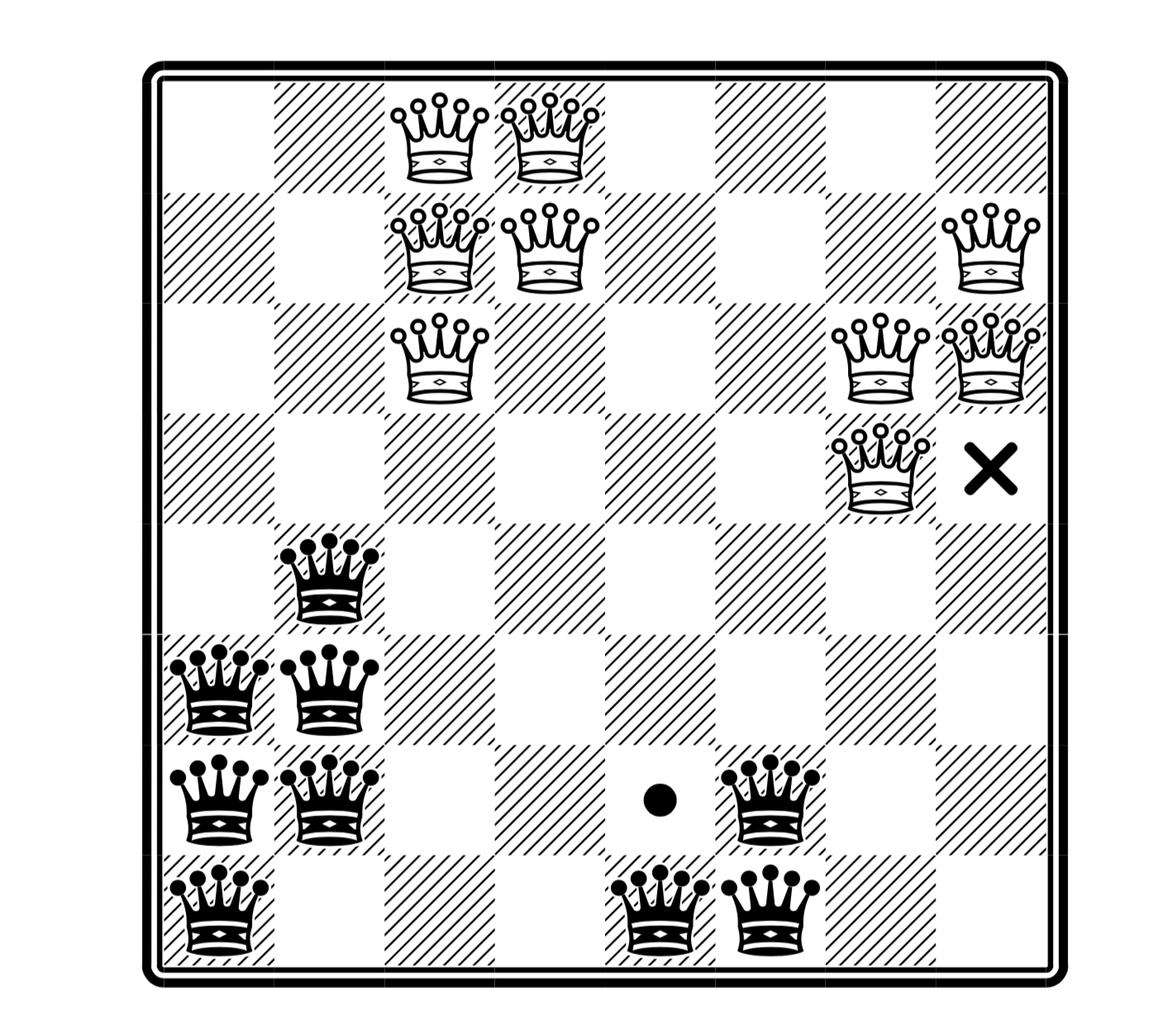
    (здесь максимальное число ферзей, причем на месте крестика можно поставить белого, а на месте точке черного — но не обоих сразу; взято из статьи)

    Модели и сложность задач

    Пришло время собственно обсудить: а как это вообще все решать и насколько быстро это вообще можно сделать?

    Линейный поиск для классической задачи

    Самый интересный момент, что даже специалисты иногда путаются и думают, что для решения N-ферзей нужен комбинаторный поиск и думают, что сложность задачи выше P. Про то, что такое P и NP, когда-то уже писал на Хабре: Зачем нам всем нужен SAT и все эти P-NP (часть первая) и . Однако, задача решается без перебора вариантов! Т.е., для доски любого размера можно всегда расставить ферзей один за одним лесенкой:

    Существует целый ряд алгоритмов расстановки, например см. вот эту статью или .

    Отсюда вывод, для N = 1 и N > 3 решение всегда есть (см. алго), а для N = 2 или N = 3
    всегда нет (тривиально следует из доски). Это значит, что задача разрешимости для N ферзей (где нужно сказать есть решение или нет) решается тривиально за константное время (ну ок, конструктивно за линейное — расставить/проверить).

    Самое время перепроверить прочитанное, читаем типичный заголовок «задачу о N ферзях признали NP-полной задачей» — у вас замироточили глаза?

    Как считать число решений на практике

    Вот тут начинается самое интересное: у количества решений задачи о расстановке ферзей даже есть своё имя — «последовательность A000170». На этом хорошие новости заканчиваются. Сложность задачи: выше NP и P#, на практике это означает, что оптимальное решение — это скачать данные последовательности в словарь и возвращать нужное число. Так как для N=27 оно уже считалось на параллельном кластере сколько там недель.

    Решение: выписываем табличку и по n, возвращаем а(n)
    n a(n)
    1: 1
    2: 0
    3: 0
    4: 2
    5: 10
    6: 4
    7: 40
    8: 92
    9: 352
    10: 724
    …
    21: 314666222712
    22: 2691008701644
    23: 24233937684440
    24: 227514171973736
    25: 2207893435808352
    26 22317699616364044
    27: 234907967154122528

    Однако, если у вас какая-то хитрая разновидность задачи и все-таки нужно посчитать решения (а их количество неизвестно и раньше их никто не посчитал), то лучший вариант прототипа обсуждается чуть ниже.

    Дополнение до N и Answer Set Programming

    Тут начинается самое интересное: в чём же состоит новый результат статьи? Задача о дополнении до N ферзей — NP-полна! (Интересно, что про NP-полноту дополнения латинского квадрата было известно ещё в 1984-ом году.)

    Что это означает на практике? Самый простой способ решишь эту задачу (или вдруг, если нам нужно её вариацию) — использовать SAT. Однако, мне больше нравится следующая аналогия:

    SAT — это ассемблер для комбинаторных NP-задач, а Answer Set Programming (ASP) — это С++ (у ASP тоже загадочная русская душа: он временами запутан и непредсказуем для непосвященных; кстати, теория, лежащая в основе современного ASP, была придумана в 1988ом году Михаилом Гельфондом и Владимиром Лифшицем, работавших тогда в университетах Техаса и Стэнфорда соответственно).

    Если говорить упрощенно: ASP — это декларативный язык программирования ограничений (constraints в англоязычной литературе) с синтаксисом Prolog. То есть мы записываем, каким ограничениям должно удовлетворять решение, а система сводит всё к варианту SAT и находит нам решение.

    Детали решения здесь не столь важны, и Answer Set Programming достоин отдельного поста (который лежит у меня в черновике уже неприлично долго): поэтому разберем концептуальные моменты

    % domain row(1..n). column(1..n). % alldifferent 1 { queen(X,Y) : column(Y) } 1 :- row(X). 1 { queen(X,Y) : row(X) } 1 :- column(Y). % remove conflicting answers :- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 == Y2. :- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 + X1 == Y2 + X2. :- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 — X1 == Y2 — X2.

    Строка 1 { queen(X,Y) : column(Y) } 1 :- row(X). — называется choice rule, и она определяет, что является допустимым пространством поиска.

    Последние три строки называются integrity constraints: и они определяют каким ограничениям должно удовлетворять решение: не может быть ферзя в одном и том же ряду, не может быть ферзя в одной и той же колонке (опущено, в силу симметрии) и не может быть ферзя на одной и той же диагонали.

    В качестве системы для экспериментов рекомендую Clingo.
    И для начала стоит посмотреть их tutorial и попочитать блог на www.hakank.org.

    Безусловно, если впервые писать на ASP, то первая модель не выйдет невероятно эффективной и быстрой, но скорее всего будет быстрее перебора с возвратом, написанным на скорую руку. Однако, если понять основные принципы работы системы, ASP может стать «regexp для NP-полных задач».

    Проведем простой численный эксперимент с нашей ASP моделью. Я добавил 5 коварных ферзей в модель и запустил поиск решения для N от 1 до 150 и вот, что вышло (запущено на обычном домашнем ноутбуке):

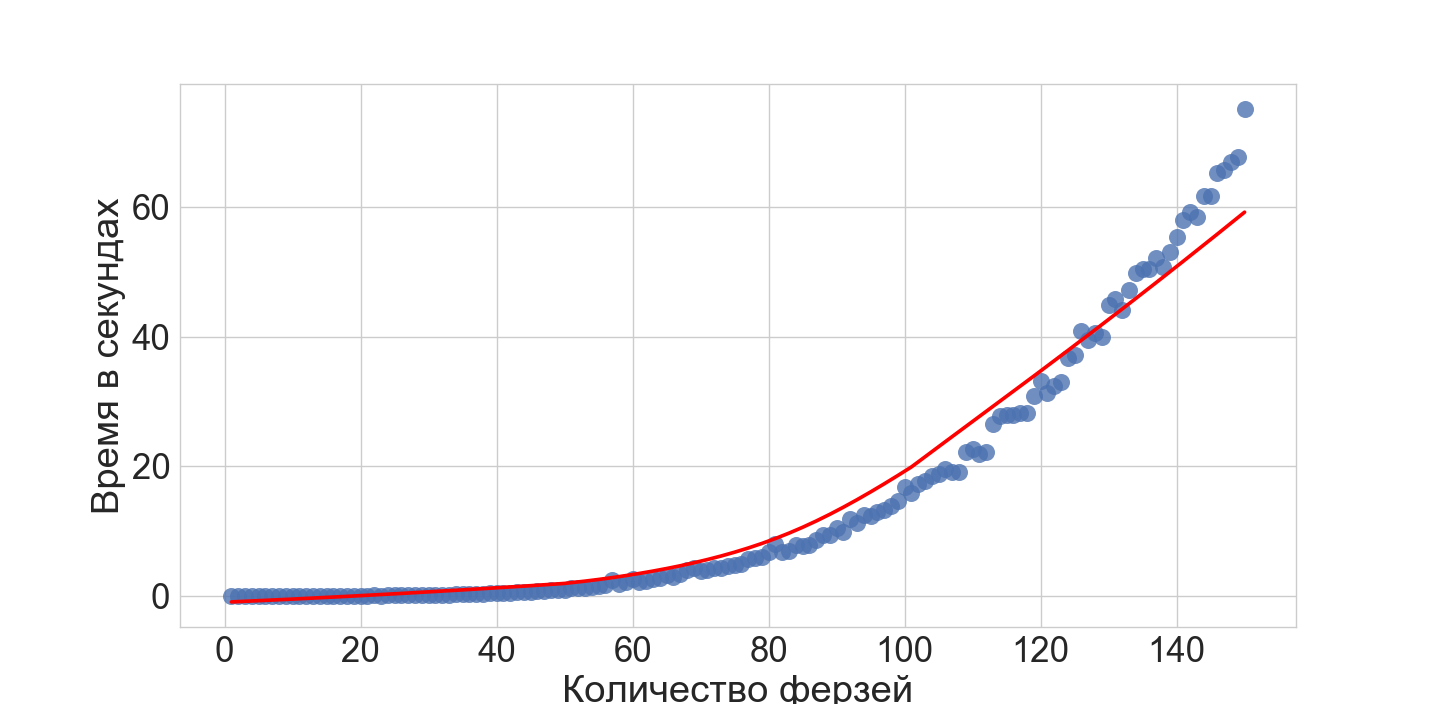
    Итого, наша ASP модель примерно в течении минуты может найти решения задачи о дополнении при N <= 150 (в обычном случае). Это показывает, что система отлично подходит для прототипирования моделей сложных комбинаторных задач.

    8.7 Понятие сложности вычислений. Np- полные задачи.

    NP-полные задачи

    При обсуждении класса NP следует иметь в виду, что наше мнение, согласно которому их решение требует большого времени, основано на том, что мы просто не нашли эффективных алгоритмов их решения. Может быть, посмотрев на задачу коммивояжера с другой точки зрения, мы смогли бы разработать полиномиальный алгоритм ее решения. То же самое можно сказать и про другие задачи, которые мы будем рассматривать в следующем параграфе.

    Термин NP-полная относится к самым сложным задачам в классеNP. Эти задачи выделены тем, что если нам все-таки удастся найти полиномиальный алгоритм решения какой-либо из них, то это будет означать, что все задачи класса NP допускают полиномиальные алгоритмы решения.

    Мы показываем, что задача является NP-полной, указывая способ выведения к ней всех остальных задач класса NP. На практике эта деятельность выглядит не столь уж устрашающе — нет необходимости осуществлять редукцию для каждой NP задачи. Вместо этого для того, чтобы доказать NP-полноту некоторой NP задачи А, достаточно свести к ней какую-нибудь NP-полную задачу В. Редуцировав задачу В к задаче А, мы показываем, что и любая NP задача может быть сведена к А за два шага, первый из которых ее редукция к В.

    В предыдущем разделе мы выполняли редукцию полиномиального алгоритма. Посмотрим теперь на редукцию алгоритма, решающего NP задачу. Нам понадобится процедура, которая преобразует все со­ставные части задачи в эквивалентные составные части другой задачи. Такое преобразование должно сохранять информацию: всякий раз, ко­гда решение первой задачи дает положительный ответ, такой же ответ должен быть и во второй задаче, и наоборот.

    Гамильтоновым путем в графе называется путь, проходящий через каждую вершину в точности один раз. Если при этом путь возвраща­ется в исходную вершину, то он называется гамильтоновым циклом. Граф, в котором есть гамильтонов путь или цикл, не обязательно явля­ется полным. Задача о поиске гамильтонова цикла следующим образом сводится к задаче о коммивояжере. Каждая вершина графа — это го­род. Стоимость пути вдоль каждого ребра графа положим равной 1. Стоимость пути между двумя городами, не соединенными ребром, по­ложим равной 2. А теперь решим соответствующую задачу о комми­вояжере. Если в графе есть гамильтонов цикл, то алгоритм решения задачи о коммивояжере найдет циклический путь, состоящий из ребер веса 1. Если же гамильтонова цикла нет, то в найденном пути будет по крайней мере одно ребро веса 2. Если в графе N вершин, то в нем есть гамильтонов цикл, если длина найденного пути равна N, и такого цикла нет, если длина найденного пути больше N.

    В 1971 году Кук доказал NP-полноту обсуждаемой в следующем пара­графе задачи о конъюнктивной нормальной форме. NP-полнота большого числа задач была доказана путем редукции к ним задачи о конъюнктив­ной нормальной форме. В книге Гэри и Джонсона, опубликованной в 1979 году, приведены сотни задач, NP-полнота которых доказана.

    Редукция — настолько мощная вещь, что если любую из NP-полных задач удастся свести к задаче класса Р, то и все NP задачи получат полиномиальное решение. До сих пор ни одна из попыток построить такое сведение не удалась.

    Типичные NP задачи

    Каждая из задач, которые мы будем обсуждать, является либо опти­мизационной, либо задачей о принятии решения. Целью оптимизацион­ной задачи обычно является конкретный результат, представляющий собой минимальное или максимальное значение. В задаче о принятии решения обычно задается некоторое пограничное значение, и нас ин­тересует, существует ли решение, большее (и задачах максимизации) или меньшее (в задачах минимизации) указанной границы. Ответом в задачах оптимизации служит полученный конкретный результат, а в задачах о принятии решений — «да» или «нет».

    Ранее мы занимались оптимизационным вариантом задачи о комми­вояжере. Это задача минимизации, и нас интересовал путь минималь­ной стоимости. В варианте принятия решения мы могли бы спросить, существует ли путь коммивояжера со стоимостью, меньшей заданной константы С. Ясно, что ответ в задаче о принятии решения зависит от выбранной границы. Если эта граница очень велика (например, она превышает суммарную стоимость всех дорог), то ответ «да» получить несложно. Если эта граница чересчур мала (например, она меньше сто­имости дороги между любыми двумя городами), то ответ «нет» также дается легко. В остальных промежуточных случаях время поиска от­вета очень велико и сравнимо со временем решения оптимизационной задачи. Поэтому мы будем говорить вперемешку о задачах оптимиза­ции и принятия решений, используя ту из них, которая точнее отвечает нашим текущим целям.

    В следующих нескольких разделах мы опишем еще шесть NP за­дач — как в оптимизационном варианте, так и в варианте принятия решения.

    Раскраска графа

    Как мы уже говорили, граф G= (V, Е) представляет собой набор вершин, или узлов, V и набор ребер Е соединяющих вершины по­парно. Здесь мы будем заниматься только неориентированными графа­ми. Вершины графа можно раскрасить в разные цвета, которые обычно обозначаются целыми числами. Нас интересуют такие раскраски, в ко­торых концы каждого ребра окрашены разными цветами. Очевидно, что в графе с N вершинами можно покрасить вершины в N различных цветов, но можно ли обойтись меньшим количеством цветов? В задаче оптимизации нас интересует минимальное число цветов, необходимых для раскраски вершин графа. В задаче принятия решения нас интере­сует, можно ли раскрасить вершины в С или менее цветов.

    У задачи о раскраске графа есть практические приложения. Если каждая вершина графа обозначает читаемый в колледже курс, и вер­шины соединяются ребром, если есть студент, слушающий оба курса, то получается весьма сложный граф. Если предположить, что каждый студент слушает 5 курсов, то на студента приходится 10 ребер. Пред­положим, что на 3500 студентов приходится 500 курсов. Тогда у полу­чившегося графа будет 500 вершин и 35 000 ребер. Если на экзамены отведено 20 дней, то это означает, что вершины графа нужно раскра­сить в 20 цветов, чтобы ни у одного студента не приходилось по два экзамена в день.

    Разработка бесконфликтного расписания экзаменов эквивалентна раскраске графов. Однако задача раскраски графов принадлежит к классу NP, поэтому разработка бесконфликтного расписания за разум­ное время невозможна. Кроме того при планировании экзаменов обыч­но требуется, чтобы у студента было не больше двух экзаменов в день, а экзамены по различным частям курсам назначаются в один день. Оче­видно, что разработка «совершенного» плана экзаменов невозможна, и поэтому необходима другая техника для получения по крайней мере неплохих планов.

    Раскладка по ящикам

    Пусть у нас есть несколько ящиков единичной емкости и набор объ­ектов различных размеров 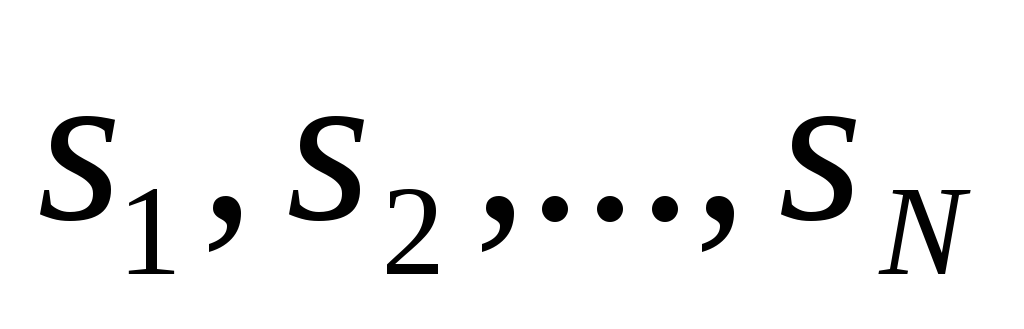. В задаче оптимизации нас ин­тересует наименьшее количество ящиков, необходимое для раскладки всех объектов, а в задаче принятия решения — можно ли упаковать все объекты в В или менее ящиков.

    Эта задача возникает при записи информации на диске или во фрагментированной памяти компьютера, при эффективном распределении груза на кораблях, при вырезании кусков из стандартных порций мате­риала по заказам клиентов. Если, например, у нас есть большие метал­лические листы и список заказов на меньшие листы, то естественно мы хотим распределить заказы как можно плотнее, уменьшив тем самым потери и увеличив доход.

    Упаковка рюкзака

    У нас имеется набор объектов объемом стоимости. В задаче оптимизации мы хотим упаковать рюкзак объемом К так, чтобы его стоимость была максимальной. В задаче принятия решения нас интересует, можно ли добиться, чтобы суммарная стоимость упа­кованных объектов была по меньшей мереW.

    Эта задача возникает при выборе стратегии вложения денег: объемом здесь является объем различных вложений стоимостью — предполагаемая величина дохода, а объем рюкзака определяется размером планируемых капиталовложений.

    Задача о суммах элементов подмножеств

    Пусть у нас есть множество объектов различных размеров и некоторая положительная верхняя границаL. В задаче оптимиза­ции нам необходимо найти набор объектов, сумма размеров которых наиболее близка к L и не превышает этой верхней границы. В задаче принятия решения нужно установить, существует ли набор объектов с суммой размеров L. Это упрощенная версия задачи об упаковке рюк­зака.

    Задача об истинности КНФ-выражения

    Конъюнктивная нормальная форма (КНФ) представляет собой по­следовательность булевских выражений, связанных между собой опера­торами AND(обозначаемыми), причем каждое выражение является мономом от булевских переменных или их отрицаний, связанных опе­раторамиOR(которые обозначаются через). Вот пример булевского выражения в конъюнктивной нормальной форме (отрицание обознача­ется чертой над именем переменной):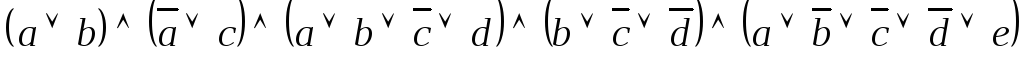

    .

    Задача об истинности булевского выражения в конъюнктивной нор­мальной форме ставится только в варианте принятия решения: суще­ствуют ли у переменных, входящих в выражение, такие значения ис­тинности, подстановка которых делает все выражение истинным. Как число переменных, так и сложность выражения не ограничены, поэтому число комбинаций значений истинности может быть очень велико.

    Задача планирования работ

    Пусть у нас есть набор работ, и мы знаем время, необходимое для завершения каждой из них, 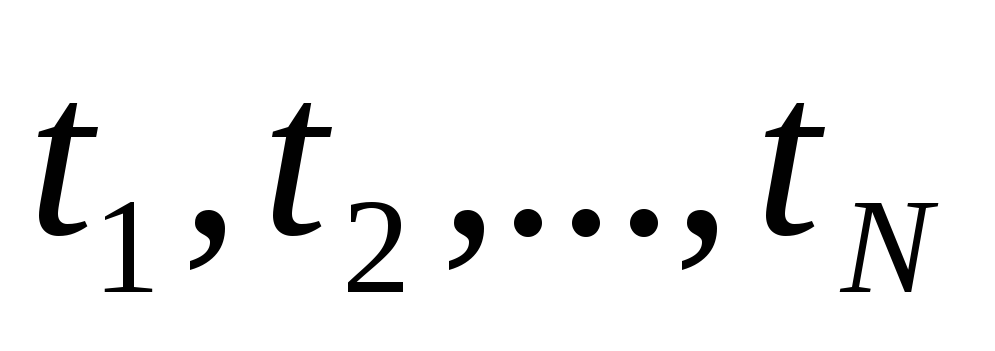, сроки, к которым эти работы должны быть обязательно завершены, а также штрафы, которые будут наложены при незавершении каждой работы в установленные сроки. Задача оптимизации требует установить порядок работ, минимизирующий накладываемые штрафы. В задаче принятия решений мы спрашиваем, есть ли порядок работ, при котором величина штрафа будет не больше Р.

    Формальное определение

    Алфавитом называется всякое конечное множество символов (например, или ). Множество всех возможных слов (конечных строк, составленных из символов этого алфавита) над некоторым алфавитом обозначается . Языком над алфавитом называется всякое подмножество множества , то есть .

    Задачей распознавания для языка называется определение того, принадлежит ли данное слово языку .

    Язык называется сводимым (по Карпу) к языку , если существует функция, , вычислимая за полиномиальное время, обладающая следующим свойством:

    • тогда и только тогда, когда

    Сводимость по Карпу обозначается как или .

    Язык называется NP-трудным, если любой язык из класса NP сводится к нему. Язык называют NP-полным, если он NP-труден, и при этом сам лежит в классе NP.

    Таким образом, если будет найден алгоритм, решающий некоторую (любую) NP-полную задачу за полиномиальное время, то все NP-задачи окажутся в классе P, то есть будут решаться за полиномиальное время.

    NP-полнота в сильном смысле

    Задача называется NP-полной в сильном смысле, если у неё существует подзадача, которая:

    1. не является задачей с числовыми параметрами (т.е. максимальное значение величин, встречающихся в этой задаче ограничено сверху полиномом от длины входа),
    2. принадлежит классу NP,
    3. является NP-полной.

    Класс таких задач называется NPCS. Если гипотеза P ≠ NP верна, то для NPCS задачи не существует псевдополиномиального алгоритма.

    Ссылки

    • NP-полнота
    • Вычислительная сложность игр и головоломок (англ.)
    • A compendium of NP optimization problems. Editors — Pierluigi Crescenzi, Viggo Kann (англ.)

    Для улучшения этой статьи желательно?:

    • Проставив сноски, внести более точные указания на источники.

    Cчитаются лёгкими

    P • L • NL • AC • NC • P-complete • BQP • BPP • RP • ZPP

    Предпологаются сложными

    NP (co-NP • NP-complete • co-NP-complete ) • UP • #P (#P-complete ) • IP • PSPACE (PSPACE-complete) • R • PP • AM

    Cчитаются сложными

    EXPTIME • NEXPTIME • EXPSPACE • 2-EXPTIME • PR • RE • Co-RE • RE-complete • Co-RE-complete • PH

    Список алгоритмов

    NP-полные задачи

    Математика

    Исследование операций:Оптимизация:Комбинаторная оптимизация

    Максимизационная задача
    укладки (упаковки)

    Упаковка в контейнеры (двумерная упаковка • линейная упаковка • упаковка по весу • упаковка по стоимости) • Задача о ранце (рюкзаке)

    Теория графов
    теория множеств

    Задача о вершинном покрытии • Задача о клике • Задача о независимом множестве (наборе) • Задача о покрытии множества • Задача Штейнера • Задача коммивояжёра • Обобщённая задача коммивояжёра

    Алгоритмические задачи

    Задача выполнимости булевых формул (в конъюнктивной нормальной форме)

    Логические игры
    и головоломки

    Обобщённые пятнашки с костяшками >15) (задача поиска кратчайшего решения) • Задачи, решения которых применяются в Тетрис • Задача обобщённого судоку • Задача о заполнении латинского квадрата • Задача какуро

    См. также

    Прикладная математика • Теория алгоритмов • Динамическое программирование • 21 NP-полная задача Карпа

    Классы сложности

    Особенности решения

    Общее число возможных расположений 8 ферзей на 64-клеточной доске равно 4 426 165 368 = (64!/(8!(64-8)!)). Общее число возможных расположений, удовлетворяющих условию задачи, равно 92. Интересно отметить, что эти 92 расположения разбиваются на 12 групп: 11 групп по 8 и одну из 4 расположений. Положения внутри групп получаются из одного положения путём преобразований симметрии: отражения от вертикальной и горизонтальной осей, отражения от диагоналей доски и поворотов на 90, 180 и 270 градусов. Пары расположений, симметричные относительно горизонтальной оси, имеют сумму номеров равную 93, то есть для каждой группы эта сумма равна 93×4.

    Современные компьютеры уже позволяют произвести решение задачи (нахождение любого или всех решений) путём прямого перебора всех возможных вариантов расстановки, но обычно такое решение считается некорректным, и от решающего задачу требуется найти алгоритм, который позволял бы существенно сократить объём перебора. Например, очевидно, что на одной горизонтали или вертикали доски не может находиться больше одного ферзя, поэтому алгоритм решения изначально не должен включать в перебор позиции, где два ферзя стоят на одной горизонтали или вертикали. Даже такое простое правило способно существенно уменьшить число возможных расположений: 16 777 216 (то есть 88) вместо 4 426 165 368. Генерируя перестановки, которые являются решениями задачи о восьми ладьях и затем проверяя атаки по диагоналям, можно сократить число возможных расположений всего до 40 320 (то есть 8!). Однако, если условие нападения по диагонали учитывать при генерации позиций, скорость счёта возрастает на порядок.

    Один из типовых алгоритмов решения задачи — использование поиска с возвратом: первый ферзь ставится на первую горизонталь, затем каждый следующий пытаются поставить на следующую так, чтобы его не били ранее установленные ферзи. Если на очередном этапе постановки свободных полей не оказывается, происходит возврат на шаг назад — переставляется ранее установленный ферзь.

    > Ссылки

    • Фрактальное решение задачи для досок N-N, если N=(a1)•(a2)•…•(an), где а1 ≥ 4 и а2,…,аn > 4 (А.Ермаков, 2011)

    Полезные статьи: