Правильная разводка сетей RS-485

Maxim’s Application Note 373 (январь 2001 года)
Переводчик Игорь Николаевич Бирюков (11 марта 2001 г.)

Rus Параметрический поиск драйверов интерфейса RS-485

Цель настоящей статьи — предоставить базовые рекомендации по выбору схемы соединений для сетей на основе RS-485. Спецификация RS-485 (официальное название TIA/EIA-485-A) не дает конкретных пояснений по поводу того, как должна осуществляться разводка сетей RS-485. Однако она предоставляет некоторые рекомендации. Эти рекомендации и инженерная практика в области обработки звука положены в основу этой статьи. Однако представленные здесь советы ни в коем случае не охватывают всего разнообразия возможных вариантов построения сетей.

RS-485 передает цифровую информацию между многими объектами. Скорость передачи данных может достигать 10 Мбит/с, а иногда и превышать эту величину. RS-485 предназначен для передачи этой информации на значительные расстояния, и 1000 метров хорошо укладывается в его возможности. Расстояние и скорость передачи данных, с которыми RS-485 может успешно использоваться, зависят от многих моментов при разработке схемы межсоединений системы.

Кабель

RS-485 спроектирован как балансная система. Проще говоря, это означает, что, помимо земляного, имеется два провода, которые используются для передачи сигнала.

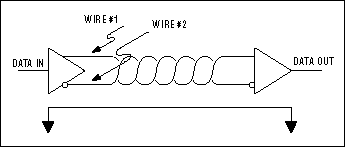
Рис. 1. Балансная система использует, помимо земляного, два провода для передачи данных.

Система называется балансной, потому что сигнал на одном проводе является идеально точной противоположностью сигнала на втором проводе. Другими словами, если один провод передает высокий уровень, другой провод будет передавать низкий уровень, и наоборот. См. Рис. 2.

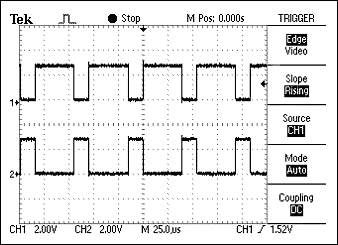
Рис. 2. Сигналы на двух проводах балансной системы идеально противоположны.

Несмотря на то, что RS-485 может успешно осуществлять передачу с использованием различных типов передающей среды, он должен использоваться с проводкой, обычно называемой «витая пара».

Что такое витая пара и почему она используется?

Как следует из ее названия, витая пара — это просто пара проводов, которые имеют равную длину и свиты вместе. Использование передатчика, отвечающего требованиям спецификации RS-485, с кабелем на основе витой пары, уменьшает два главных источника проблем для разработчиков быстродействующих территориально распределенных сетей, а именно излучаемые электромагнитные помехи и индуцируемые электромагнитные помехи (наводка).

Излучаемые электромагнитные помехи

Как показано на рисунке 3, всякий раз, когда для передачи информации используются импульсы с крутыми фронтами, в сигнале присутствуют высокочастотные составляющие. Эти крутые фронты нужны при более высоких скоростях, чем способен обеспечить RS-485.

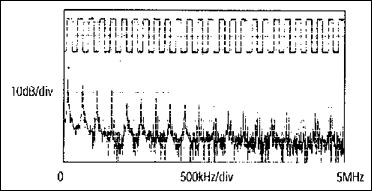
Рис. 3. Форма сигнала последовательности прямоугольных импульсов с частотой 125 кГц и ее БПФ

Полученные в итоге высокочастотные компоненты этих крутых фронтов вместе с длинными проводами могут привести к излучению электромагнитных помех (EMI). Балансная система, использующая линии связи на основе витой пары, уменьшает этот эффект, делая систему неэффективным излучателем. Это работает на очень простом принципе. Поскольку сигналы на линиях равны, но инверсны, излучаемые от каждого провода сигналы будут также иметь тенденцию быть равными, но инверсными. Это создает эффект подавления одного сигнала другим, что, в свою очередь, означает отсутствие электромагнитного излучения. Однако, это основано на предположении, что провода имеют точно одинаковую длину и точно одинаковое расположение. Поскольку невозможно одновременно иметь два провода абсолютно одинаково расположенными, провода должны быть близко друг к другу насколько возможно. Скручивание проводов помогает нейтрализовать любое остаточное электро-магнитное излучение из-за конечного расстояния между двумя проводами.

Индуцируемые электромагнитные помехи

Индуцируемые электромагнитные помехи — в основном та же самая проблема, что и излучаемые, но наоборот. Межсоединения, используемые в системе на основе RS-485, также действуют как антенна, которая получает нежелательные сигналы. Эти нежелательные сигналы могут искажать полезные сигналы, что, в свою очередь, может привести к ошибкам в данных. По той же самой причине, по которой витая пара помогает предотвращать излучение электромагнитных помех, она также поможет снизить влияние наводимых электромагнитных помех. Поскольку два провода расположены вместе и скручены, шум, наведенный на одном проводе будет иметь тенденцию быть тем же самым, что и наведенный на втором проводе. Этот тип шума называют «синфазным шумом». Поскольку приемники RS-485 предназначены для обнаружения сигналов, которые являются противоположностью друг друга, они могут легко подавлять шум, который является общим для обоих проводов.

Волновое сопротивление витой пары

В зависимости от геометрии кабеля и материалов, используемых в изоляции, витая пара будет обладать соответствующим «волновым сопротивлением (характеристическим импедансом)», которое обычно определяется ее производителем. Спецификация RS-485 рекомендует, но явно не навязывает, чтобы это волновое сопротивление было равно 120 Ом. Рекомендация этого импеданса необходима для вычисления наихудшей нагрузки и диапазонов синфазных напряжений, определенных в спецификации RS-485. По всей видимости, спецификация не диктует этот импеданс в интересах гибкости. Если по каким-либо причинам не может использоваться 120-омный кабель, рекомендуется, чтобы наихудший вариант нагрузки (допустимое число передатчиков и приемников) и наихудшие диапазоны синфазных напряжений были повторно рассчитаны, дабы удостовериться, что проектируемая система будет работать. Публикация TSB89 содержит раздел, специально посвященный таким вычислениям.

Число витых пар на каждый передатчик

Теперь, когда мы понимаем, какой нужен тип кабеля, возникает вопрос о том, каким количеством витых пар может управлять передатчик. Ответ короткий — точно одной. Хотя передатчик и может при некоторых обстоятельствах управлять более чем одной витой парой, это не предусмотрено спецификацией.

Согласующие резисторы

Поскольку затронуты высокие частоты и большие расстояния, должное внимание должно быть уделено эффектам, возникающим в линиях связи. Однако, детальное обсуждение этих эффектов и корректных методов согласования далеко выходит за рамки настоящей статьи. Помня об этом, техника согласования будет кратко рассмотрена в своей простейшей форме, постольку, поскольку она имеет отношение к RS-485.

Согласующий резистор — это просто резистор, который установлен на крайнем конце или концах кабеля (Рис. 4). В идеале, сопротивление согласующего резистора равно волновому сопротивлению кабеля.

Рис 4. Согласующие резисторы должны иметь сопротивление, равное волновому сопротивлению витой пары и должны размещаться на дальних концах кабеля.

Если сопротивление согласующих резисторов не равно волновому сопротивлению кабеля, произойдет отражение, т.е. сигнал вернется по кабелю обратно. Это описывается уравнением (Rt-Zo)/(Zo+Rt), где Zo — сопротивление кабеля, а Rt — номинал согласующего резистора. Хотя, в силу допустимых отклонений в кабеле и резисторе, некоторое отражение неизбежно, значительные расхождения могут вызвать отражения, достаточно большие для того, чтобы привести к ошибкам в данных. См. рисунок 5.

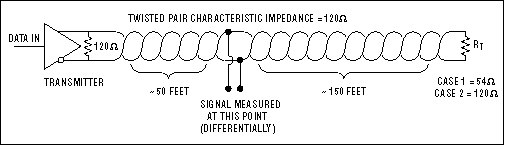
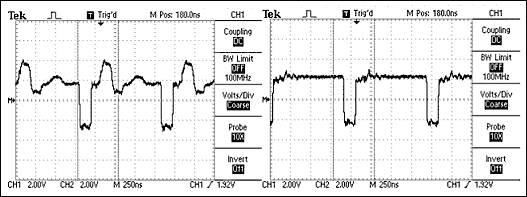
Рис. 5. Используя схему, показанную на верхнем рисунке, сигнал слева был получен с MAX3485, нагруженным на 120-омную витую пару, и 54-омным согласующим резистором. Сигнал справа был получен при корректном согласовании с помощью 120-омного резистора.

Помня об этом, важно обеспечить максимально-возможную близость значений сопротивления согласующего резистора и волнового сопротивления. Место установки согласующего резистора так-же очень важно. Согласующие резисторы должны всегда размещаться на дальних концах кабеля.

Как общее правило, согласующие резисторы должны быть помещены на обоих дальних концах кабеля. Хотя правильное согласование обоих концов абсолютно критично для большинства системных дизайнов, можно утверждать, что в одном специальном случае необходим только один согласующий резистор. Этот случай имеет место в системе, в которой имеется единственный передатчик, и этот единственный передатчик расположен на дальнем конце кабеля. В этом случае нет необходимости размещать согласующий резистор на конце кабеля с передатчиком, поскольку сигнал всегда распространяется от этого передатчика.

Максимальное число передатчиков и приемников в сети

Простейшая сеть на основе RS-485 состоит из одного передатчика и одного приемника. Хотя это и полезно в ряде приложении, но RS-485 привносит большую гибкость, разрешая более одного приемника и передатчика на одной витой паре. Допустимый максимум зависит от того, насколько каждое из устройств загружает систему.

В идеальном мире, все приемники и неактивные передатчики будут иметь бесконечный импеданс и никогда не будут нагружать систему. В реальном мире, однако, так не бывает. Каждый приемник, подключенный к сети и все неактивные передатчики увеличивают нагрузку. Чтобы помочь разработчику сети на основе RS-485 выяснить, сколько устройств могут быть добавлены к сети, была создана гипотетическая единица, называемая «единичная нагрузка (unit load)». Все устройства, которые подключаются к сети RS-485, должны характеризоваться отношением множителей или долей единичной нагрузки. Два примера — MAX3485, который специфицирован как 1 единичная нагрузка, и MAX487, который специфицирован как 1/4 единичной нагрузки. Максимальное число единичных нагрузок на витой паре (принимая, что мы имеем дело с должным образом согласованным кабелем, имеющим волновое сопротивление 120 Ом или больше) — 32. Для приведенных выше примеров это означает, что в одну сеть могут быть включены до 32 устройств MAX3485 или до 128 MAX487.

Примеры правильных сетей

Вооружившись приведенной выше информацией, мы готовы разработать некоторые сети на основе RS-485. Вот несколько простых примеров.

Один передатчик, один приемник

Простейшая сеть — это один передатчик и один приемник (Рисунок 6). В этом примере, согласующий резистор показан на кабеле на стороне передатчика. Хотя здесь это необязательно, вероятно хорошей привычкой было бы проектировать сети с обоими согласующими резисторами. Это позволят перемещать передатчик в места, отличные от дальнего конца кабеля, а также позволяет, если в этом возникнет необходимость, добавить в сеть дополнительные передатчики.

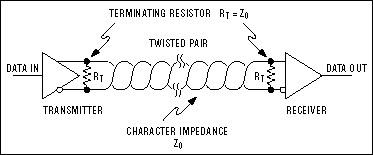
Рис. 6. Сеть RS-485 с одним передатчиком и одним приемником

Один передатчик, несколько приемников

На рисунке 7 представлена сеть с одним передатчиком и несколькими приемниками. Здесь важно, чтобы расстояния от витой пары до приемников были как можно короче.

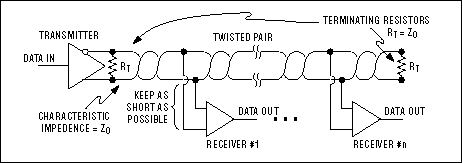
Рис. 7. Сеть RS-485 с одним передатчиком и несколькими приемниками

Два приемопередатчика

На рисунке 8 представлена сеть с двумя приемопередатчиками.

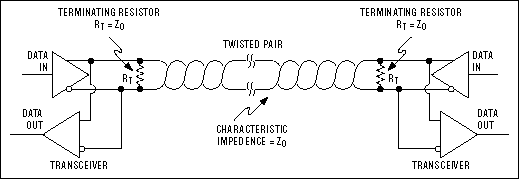
Рис. 8. Сеть RS-485 с двумя приемопередатчиками

Несколько приемопередатчиков

На рисунке 8 представлена сеть с несколькими приемопередатчиками. Как и в примере с одним передатчиком и несколькими приемниками, важно, чтобы расстояния от витой пары до приемников были как можно короче.

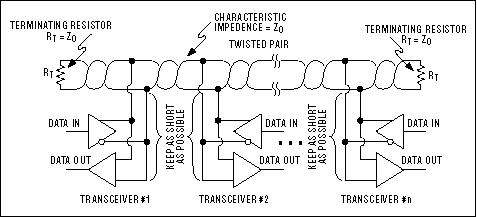
Рис. 9. Сеть RS-485 с несколькими приемопередатчиками

Примеры неправильных сетей

Ниже представлены примеры неправильно сконфигурированных систем. В каждом примере сравнивается форма сигнала, полученного от некорректно разработанной сети, с формой сигнала, полученного от должным образом разработанной системы. Форма сигнала измерялась дифференциально в точках A и B (A-B).

Несогласованная сеть

В этом примере, на концах витой пары отсутствуют согласующие резисторы. Поскольку сигнал распространяется от источника, он сталкивается с открытой цепью на конце кабеля. Это приводит к рассогласованию импедансов, вызывая отражение. В случае открытой цепи (как показано ниже), вся энергия отражается назад к источнику, вызывая сильное искажение формы сигнала.

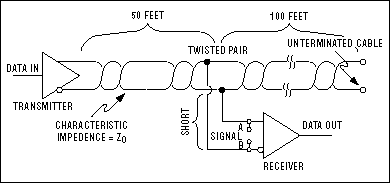
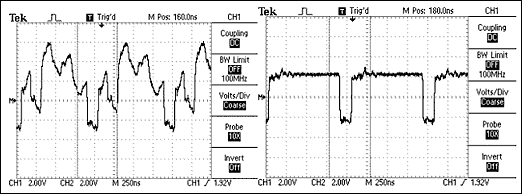
Рис. 10. Несогласованная сеть RS-485 (вверху) и ее итоговая форма сигнала (слева) по сравнению с сигналом, полученным на правильно согласованной сети (справа)

Неправильное расположение терминатора

На рисунке 11 согласующий резистор (терминатор) присутствует, но его размещение отличается от дальнего конца кабеля. Поскольку сигнал распространяется от источника, он сталкивается с двумя рассогласованиями импеданса. Первое встречается на согласующем резисторе. Даже при том, что резистор согласован с волновым сопротивлением кабеля, есть еще кабель за резистором. Этот дополнительный кабель вызывает рассогласование, а значит и отражение сигнала. Второе рассогласование, это конец несогласованного кабеля, ведет к дополнительным отражениям.

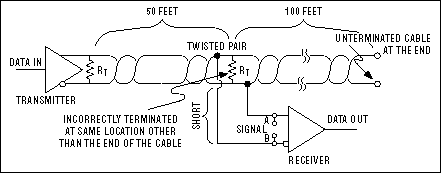
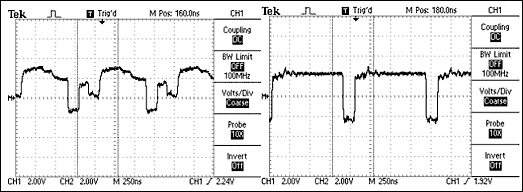
Рис. 11. Сеть RS-485 с неправильно размещенным согласующим резистором (верхний рисунок) и ее итоговая форма сигнала (слева) по сравнению с сигналом, полученным на правильно согласованной сети (справа)

Составные кабели

На рисунке 12 имеется целый ряд проблем с организацией межсоединений. Первая проблема заключается в том, что драйверы RS-485 разработаны для управления только одной, правильным образом согласованной, витой парой. Здесь же каждый передатчик управляет четырьмя параллельными витыми парами. Это означает, что требуемые минимальные логические уровни не могут гарантироваться. В дополнение к тяжелой нагрузке, имеется рассогласование импедансов в точке, где соединяются несколько кабелей. Рассогласование импедансов в очередной раз означает отражения и, как следствие, искажение сигнала.

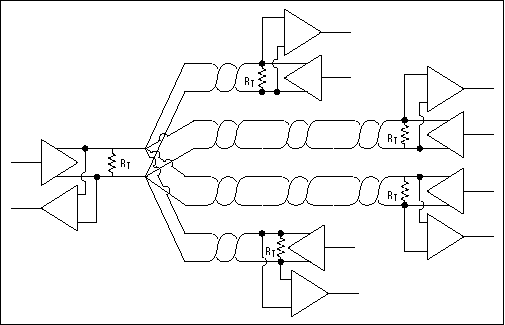
Рис. 12. Сеть RS-485, некорректно использующая несколько витых пар

Длинные ответвители

На рисунке 13, кабель корректно согласован и передатчик нагружен только на одну витую пару; однако сегмент провода в точке подключения (ответвитель — stub) приемника чрезмерно длинный. Длинные ответвители вызывают значительное рассогласование импедансов и, таким образом, отражение сигнала. Все ответвители должны быть как можно короче.

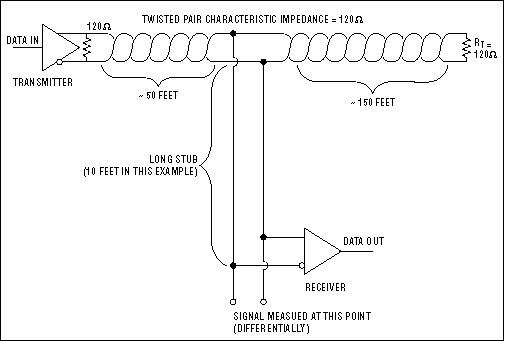
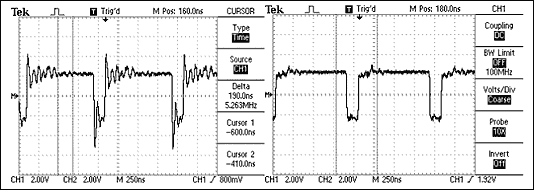
Рис. 13. Сеть RS-485 использующая 3-метровый ответвитель (рисунок сверху) и ее итоговый сигнал (слева) по сравнению с сигналом, полученным с коротким ответвлением

Длинная линия

Длинная линия — модель линии передачи, продольный размер (длина) которой превышает длину волны, распространяющейся в ней (либо сравнима с длиной волны), а поперечные размеры (например, расстояние между проводниками, образующими линию) значительно меньше длины волны.

С точки зрения теории электрических цепей длинная линия относится к четырёхполюсникам. Характерной особенностью длинной линии является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается подключенным ко входу линии генератором электромагнитных колебаний и называется падающей. Другая волна называется отражённой и возникает из-за частичного отражения падающей волны от нагрузки, подключенной к выходу (противоположному генератору концу) линии. Всё разнообразие колебательных и волновых процессов, происходящих в длинной линии, определяется соотношениями амплитуд и фаз падающей и отраженной волн. Анализ процессов упрощается, если длинная линия является регулярной, то есть такой, у которой в продольном направлении неизменны поперечное сечение и электромагнитные свойства (εr, μr, σ) заполняющих сред .

Дифференциальные уравнения длинной линии

Двухпроводная длинная линия
ZН = RН + iXН — комплексное сопротивление нагрузки;
z — продольная координата линии, отсчитываемая от места подключения нагрузки. Основная статья: Телеграфные уравнения

Первичные параметры

Из электродинамики известно, что линия передачи может быть охарактеризована её погонными параметрами:

• R1 — погонное сопротивление металла проводов, Ом/м;
• G1 — паразитная, параллельная(источник термина ) погонная(продольная, аддитивная) проводимость диэллектрика линии,1/Ом·м или См/м; ,- погонная вдоль линии, ортогонально токам утечки через диэллектрик, в противовес g — проводимости погонной,приведённой к единице длины паразитного тока, текущего через диэллектрик линии(поперечно-погонной проводимости изолятора линии)!
• L1 — погонная индуктивность Гн/м;
• C1 — погонная ёмкость Ф/м;
• Z 1 = R 1 + i ω L 1 {\displaystyle Z_{1}=R_{1}+i\omega L_{1}}
• Y 1 = G 1 + i ω C 1 {\displaystyle Y_{1}=G_{1}+i\omega C_{1}}

Погонные сопротивление и проводимость G1 зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Согласно закону Джоуля — Ленца, чем меньше тепловые потери в металле проводов и в диэлектрике, тем меньше погонное сопротивление металла R1 и меньше погонная проводимость диэлектрика G1. (Уменьшение активных потерь в диэлектрике означает увеличение его сопротивления, так как активные потери в диэлектрике — это токи утечки. Для модели используется обратная величина — погонная проводимость G1.)

Погонные индуктивность L1 и ёмкость C1 определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними.

А Z 1 {\displaystyle Z_{1}} и Y 1 {\displaystyle Y_{1}} — погонные комплексные сопротивление и проводимость линии, зависящие от частоты ω {\displaystyle \omega } .

Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему.

Эквивалентная схема участка длинной линии

Эквивалентная схема участка длинной линии. Стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI — приращения напряжения и тока в линии на элементе длины dz

Значения параметров схемы определяются соотношениями:

{ d R = R 1 d z ; d G = G 1 d z ; d L = L 1 d z ; d C = C 1 d z ; {\displaystyle {\begin{cases}dR=R_{1}dz;\\dG=G_{1}dz;\\dL=L_{1}dz;\\dC=C_{1}dz;\\\end{cases}}}

(1)

Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:

{ d U = − I ( d R + i ω d L ) d I = − U ( d G + i ω d C ) {\displaystyle {\begin{cases}dU=-I(dR+i\omega dL)\\dI=-U(dG+i\omega dC)\\\end{cases}}}

Подставляя сюда значения параметров схемы из (1), получаем:

{ d U = − I Z 1 d z d I = − U Y 1 d z {\displaystyle {\begin{cases}dU=-IZ_{1}dz\\dI=-UY_{1}dz\\\end{cases}}}

Из последних соотношений находим дифференциальные уравнения линии. Эти уравнения определяют связь между током и напряжением в любом сечении линии и называются телеграфными уравнениями длинной линии:

Телеграфные уравнения

{ d U d z = − I Z 1 d I d z = − U Y 1 {\displaystyle {\begin{cases}{\frac {dU}{dz}}=-IZ_{1}\\{\frac {dI}{dz}}=-UY_{1}\\\end{cases}}}

(2)

Следствия

Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z:

{ d 2 U d z 2 = − d I d z Z 1 d 2 I d z 2 = − d U d z Y 1 {\displaystyle {\begin{cases}{\frac {d^{2}U}{dz^{2}}}=-{\frac {dI}{dz}}Z_{1}\\{\frac {d^{2}I}{dz^{2}}}=-{\frac {dU}{dz}}Y_{1}\\\end{cases}}}

(3)

При этом учтем условие регулярности линии:

Условие регулярности линии

{ d Z 1 d z = 0 d Y 1 d z = 0 {\displaystyle {\begin{cases}{\frac {dZ_{1}}{dz}}=0\\{\frac {dY_{1}}{dz}}=0\\\end{cases}}}

(4)

Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (4) состоит в неизменности вдоль линии её погонных параметров.

Подставляя в (3) значения производных напряжения и тока из (2), после преобразований получаем:

Однородные волновые уравнения длинной линии

{ d 2 U d z 2 − γ 2 U = 0 d 2 I d z 2 − γ 2 I = 0 {\displaystyle {\begin{cases}{\frac {d^{2}U}{dz^{2}}}-\gamma ^{2}U=0\\{\frac {d^{2}I}{dz^{2}}}-\gamma ^{2}I=0\\\end{cases}}} ,

(5)

где γ = Z 1 Y 1 {\displaystyle \gamma ={\sqrt {Z_{1}Y_{1}}}} — коэффициент распространения волны в линии.

Соотношения (5) называются однородными волновыми уравнениями длинной линии. Их решения известны и могут быть записаны в виде:

{ U = B U e γ z + A U e − γ z I = B I e γ z + A I e − γ z {\displaystyle {\begin{cases}U=B_{U}e^{\gamma z}+A_{U}e^{-\gamma z}\\I=B_{I}e^{\gamma z}+A_{I}e^{-\gamma z}\\\end{cases}}} ,

(6)

где AU, BU и AI, BI — коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.

Решения волновых уравнений в виде (6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой отраженную волну напряжения или тока, распространяющуюся от нагрузки к генератору, второе слагаемое — падающую волну, распространяющуюся от генератора к нагрузке. Таким образом, коэффициенты AU, AI представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты BU, BI — комплексные амплитуды отраженных волн напряжения и тока соответственно. Так как часть мощности, передаваемой по линии, может поглощаться в нагрузке, то амплитуды отраженных волн не должны превышать амплитуды падающих:

| B U | ⩽ | A U | {\displaystyle |B_{U}|\leqslant |A_{U}|}| B I | ⩽ | A I | {\displaystyle |B_{I}|\leqslant |A_{I}|}

Направление распространения волн в (6) определяется знаком в показателях степени экспонент: плюс — волна распространяется в отрицательном направлении оси z; минус — в положительном направлении оси z (см. рис. 1). Так, например, для падающих волн напряжения и тока можно записать:

{ U Π = A U e − γ z I Π = A I e − γ z {\displaystyle {\begin{cases}U_{\Pi }=A_{U}e^{-\gamma z}\\I_{\Pi }=A_{I}e^{-\gamma z}\\\end{cases}}} ,

(7)

Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен в виде:

γ = Z 1 Y 1 = ( R 1 + i ω L 1 ) ( G 1 + i ω C 1 ) = α + i β {\displaystyle \gamma ={\sqrt {Z_{1}Y_{1}}}={\sqrt {(R_{1}+i\omega L_{1})(G_{1}+i\omega C_{1})}}=\alpha +i\beta } ,

(8)

где α — коэффициент затухания волны в линии; β — коэффициент фазы. Тогда соотношение (7) можно переписать в виде:

{ U Π = A U e − α z e − i β z I Π = A I e − α z e − i β z {\displaystyle {\begin{cases}U_{\Pi }=A_{U}e^{-\alpha z}e^{-i\beta z}\\I_{\Pi }=A_{I}e^{-\alpha z}e^{-i\beta z}\\\end{cases}}} .

(9)

Так как при распространении падающей волны на длину волны в линии λЛ фаза волны изменяется на 2π, то коэффициент фазы можно связать с длиной волны λЛ соотношением

β = 2 π λ Λ {\displaystyle \beta ={\frac {2\pi }{\lambda _{\Lambda }}}} .

(10)

При этом фазовая скорость волны в линии VФ определяется через коэффициент фазы:

V Φ = ω β {\displaystyle V_{\Phi }={\frac {\omega }{\beta }}} .

(11)

Определим коэффициенты A и B, входящие в решения (6) волновых уравнений, через значения напряжения UН и тока IН на нагрузке. Это является оправданным, так как напряжение и ток на нагрузке практически всегда можно измерить с помощью измерительных приборов. Воспользуемся первым из телеграфных уравнений (2) и подставим в него напряжение и ток из (6). Тогда получим:

A U γ e − γ z − B U γ e γ z = Z 1 ( A I e − γ z + B I e γ z ) {\displaystyle A_{U}\gamma e^{-\gamma z}-B_{U}\gamma e^{\gamma z}=Z_{1}(A_{I}e^{-\gamma z}+B_{I}e^{\gamma z})}

Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:

{ A I = A U W B I = − B U W {\displaystyle {\begin{cases}A_{I}={\frac {A_{U}}{W}}\\B_{I}=-{\frac {B_{U}}{W}}\\\end{cases}}} ,

(12)

где W = Z 1 Y 1 {\displaystyle W={\sqrt {\frac {Z_{1}}{Y_{1}}}}} — волновое сопротивление линии.

Перепишем (6) с учётом (12):

Для определения коэффициентов A и B в этих уравнениях воспользуемся условиями в начале линии z = 0:

{ U ( z = 0 ) = U H I ( z = 0 ) = I H {\displaystyle {\begin{cases}U(z=0)=U_{H}\\I(z=0)=I_{H}\\\end{cases}}}.

Тогда из (13) при z = 0 найдем

{ A U = 1 2 ( U H + I H W ) B U = 1 2 ( U H − I H W ) {\displaystyle {\begin{cases}A_{U}={\tfrac {1}{2}}(U_{H}+I_{H}W)\\B_{U}={\tfrac {1}{2}}(U_{H}-I_{H}W)\\\end{cases}}} ,

(14)

Подставив полученные значения коэффициентов из (14) в (13), после преобразований получим:

При выводе (15) учтены определения гиперболических синуса и косинуса.

Соотношения для напряжения и тока (15) так же, как и (6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (6) определены через амплитуды падающей и отраженной волн, а в (15) — через напряжение и ток на нагрузке.

Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует. Тогда в (6) следует положить BU = 0, BI = 0:

{ U = A U e − α z e − i β z I = A I e − α z e − i β z {\displaystyle {\begin{cases}U=A_{U}e^{-\alpha z}e^{-i\beta z}\\I=A_{I}e^{-\alpha z}e^{-i\beta z}\\\end{cases}}}.

Распределение поля падающей волны

Рис.3. Эпюры напряжений падающей волны в длинной линии. а) амплитуда; б) фаза

На рис.3. представлены эпюры изменения амплитуды |U| и фазы φU напряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (α = 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (α > 0) часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении распространения.

Фаза напряжения падающей волны φU = β z изменяется по линейному закону и уменьшается по мере удаления от генератора.

Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, то есть α = 0. Тогда напряжение в линии можно представить в виде:

U = A U e − i β z + B U e i β z = A U ( e − i β z + Γ e i β z ) {\displaystyle U=A_{U}e^{-i\beta z}+B_{U}e^{i\beta z}=A_{U}(e^{-i\beta z}+\Gamma e^{i\beta z})} ,

(16)

где Γ = B U / A U {\displaystyle \Gamma =B_{U}/A_{U}} — комплексный коэффициент отражения по напряжению.

Комплексный коэффициент отражения по напряжению

Характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах: 0 ⩽ | Γ | ⩽ 1 {\displaystyle 0\leqslant |\Gamma |\leqslant 1}

• | Г | = 0, если отражения от нагрузки отсутствуют и BU = 0;
• | Г | = 1, если волна полностью отражается от нагрузки, то есть | A U | = | B U | {\displaystyle |A_{U}|=|B_{U}|} ;

Соотношение (16) представляет собой сумму падающей и отраженной волн.

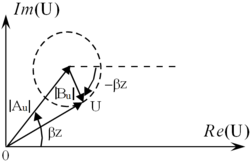Рис.4. Векторная диаграмма напряжений в линии с отраженной волной

Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 4). Из диаграммы видно, что существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн:

U m a x = | A U | + | B U | {\displaystyle U_{max}=|A_{U}|+|B_{U}|}.

Кроме того, существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума:

U m i n = | A U | − | B U | {\displaystyle U_{min}=|A_{U}|-|B_{U}|}.

Если линия нагружена на сопротивление, для которого |Г| = 1, то есть амплитуда падающей и отраженной волн равны |BU| = |AU|, то в этом случае Umax = 2|AU|, а Umin = 0.

Рис.5. Эпюры распределения напряжения вдоль линии с отражённой волной. а) Модуль напряжения; б) фаза напряжения.

Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 5 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.

Линия без потерь

В линии без потерь погонные параметры R1 = 0 и G1 = 0. Поэтому для коэффициента распространения γ и волнового сопротивления W получим:

С учётом этого выражения для напряжения и тока (15) примут вид:

При выводе этих соотношений учтены особенности гиперболических функций.

Рассмотрим конкретные примеры работы линии без потерь на простейшие нагрузки.

Разомкнутая линия

Рис.6. Эпюры напряжения, тока и входного сопротивления в открытой (разомкнутой) линии

В этом случае ток, протекающий через нагрузку равен нулю (IН = 0), поэтому выражения для напряжения, тока и входного сопротивления в линии принимают вид:

На рис.6 эти зависимости проиллюстрированы графически. Из соотношений (22) и графиков следует:

• в линии, разомкнутой на конце, устанавливается режим стоячей волны, напряжение, ток и входное сопротивление вдоль линии изменяются по периодическому закону с периодом λЛ/2;
• входное сопротивление разомкнутой линии является чисто мнимым за исключением точек с координатами z = nλЛ/4, n = 0,1,2,…;
• если длина разомкнутой линии меньше λЛ/4, то такая линия эквивалентна ёмкости;
• разомкнутая на конце линия длиной λЛ/4 эквивалентна последовательному резонансному на рассматриваемой частоте контуру и имеет нулевое входное сопротивление;
• линия, длина которой лежит в интервале от λЛ/4 до λЛ/2, эквивалентна индуктивности;
• разомкнутая на конце линия длиной λЛ/2 эквивалентна параллельному резонансному контуру на рассматриваемой частоте и имеет бесконечно большое входное сопротивление.

Замкнутая линия

Рис.7. Эпюры напряжений, тока и входного сопротивления в короткозамкнутой линии

В этом случае напряжение на нагрузке равно нулю (UН = 0), поэтому напряжение, ток и входное сопротивление в линии принимают вид:

На рис.7 эти зависимости проиллюстрированы графически.

Используя результаты предыдущего раздела, нетрудно самостоятельно сделать выводы о трансформирующих свойствах короткозамкнутой линии. Отметим лишь, что в замкнутой линии также устанавливается режим стоячей волны. Отрезок короткозамкнутой линии, длиной меньше λЛ/4 имеет индуктивный характер входного сопротивления, а при длине λЛ/4 такая линия имеет бесконечно большое входное сопротивление на рабочей частоте.

Ёмкостная нагрузка

Рис.8. Эпюры напряжения, тока и входного сопротивления в линии, нагруженной на ёмкость

Как следует из анализа работы разомкнутой линии, каждой ёмкости C на данной частоте ω можно поставить в соответствие отрезок разомкнутой линии длиной меньше λЛ/4. Ёмкость C имеет ёмкостное сопротивление i X C = − i ω C {\displaystyle iX_{C}=-{\tfrac {i}{\omega C}}} . Приравняем величину этого сопротивления к входному сопротивлению разомкнутой линии длиной l < λЛ/4:

− i ω C = − i W ctg ⁡ ( β l ) {\displaystyle -{\tfrac {i}{\omega C}}=-iW\operatorname {ctg} (\beta l)}.

Отсюда находим длину линии, эквивалентную по входному сопротивлению ёмкости C:

l = 1 β arctg ⁡ ( ω C W ) {\displaystyle l={\tfrac {1}{\beta }}\operatorname {arctg} (\omega CW)}.

Зная эпюры напряжения, тока и входного сопротивления разомкнутой линии, восстанавливаем их для линии, работающей на ёмкость (рис.8). Из эпюр следует, что в линии, работающей на ёмкость, устанавливается режим стоячей волны.

При изменений ёмкости эпюры сдвигаются вдоль оси z. В частности, при увеличении ёмкости ёмкостное сопротивление уменьшается, напряжение на ёмкости падает и все эпюры сдвигаются вправо, приближаясь к эпюрам, соответствующим короткозамкнутой линии. При уменьшении ёмкости эпюры сдвигаются влево, приближаясь к эпюрам, соответствующим разомкнутой линии.

Индуктивная нагрузка

Рис.9. Эпюры напряжения, тока и входного сопротивления в линии, работающей на индуктивность

Как следует из анализа работы замкнутой линии, каждой индуктивности L на данной частоте ω можно поставить в соответствие отрезок замкнутой линии длиной меньше λЛ/4. Индуктивность L имеет индуктивное сопротивление iXЛ = iωL. Приравняем это сопротивление к входному сопротивлению замкнутой линии длиной λЛ/4:

i ω L = i W tg ⁡ ( β l ) {\displaystyle i\omega L=iW\operatorname {tg} (\beta l)}.

Отсюда находим длину линии l, эквивалентную по входному сопротивлению индуктивности L:

l = 1 β arctg ⁡ ( ω L W ) {\displaystyle l={\tfrac {1}{\beta }}\operatorname {arctg} (\omega {\tfrac {L}{W}})}.

Зная эпюры напряжения, тока и входного сопротивления замкнутой на конце линии, восстанавливаем их для линии, работающей на индуктивность (рис. 9). Из эпюр следует, что в линии, работающей на индуктивность, также устанавливается режим стоячей волны. Изменение индуктивности приводит к сдвигу эпюр вдоль оси z. Причем с увеличением L эпюры сдвигаются вправо, приближаясь к эпюрам холостого хода, а с уменьшением L — влево по оси z, стремясь к эпюрам короткого замыкания.

Активная нагрузка

В этом случае ток и напряжение на нагрузке RН связаны соотношением UН = IНRН. Выражения для напряжения и тока в линии (21) принимают вид:

Рассмотрим работу такой линии на примере анализа напряжения. Найдем из (23) амплитуду напряжения в линии:

| U | = U H cos 2 ⁡ ( β z ) + ( W R H ) 2 sin 2 ⁡ ( β z ) {\displaystyle |U|=U_{H}{\sqrt {\cos ^{2}(\beta z)+\left({\tfrac {W}{R_{H}}}\right)^{2}\sin ^{2}(\beta z)}}}

(24)

Отсюда следует, что можно выделить три случая:

• Сопротивление нагрузки равно волновому сопротивлению линии RН = W
• Сопротивление нагрузки больше волнового сопротивления линии RН > W
• Сопротивление нагрузки меньше волнового сопротивления линии RН < W

В первом случае из (24) следует |U| = UН, то есть распределение амплитуды напряжения вдоль линии остается постоянным, равным амплитуде напряжения на нагрузке. Это соответствует режиму бегущей волны в линии.

Комплексная нагрузка

> См. также

• Измерительная линия
• Металлический изолятор
• Диаграмма Вольперта — Смита

Примечания

1. ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
2. 1 2 3 4 Коэффициент затухания α определяет скорость уменьшения амплитуды волны при распространении вдоль линии.
3. Коэффициент фазы β определяет скорость изменения фазы волны вдоль линии.
4. Волновым сопротивлением линии передачи называется отношение напряжения к току в бегущей волне.
5. 1 2 Гиперболические функции
6. 1 2 3 Такая линия называется полностью согласованной.
7. 1 2 3 4 5 Не реализуемо на практике. Является лишь математической абстракцией Возможно лишь приближение в той, или иной степени.
8. ch ⁡ ( i β z ) = cos ⁡ ( β z ) {\displaystyle \operatorname {ch} (i\beta z)=\cos(\beta z)} , sh ⁡ ( i β z ) = sin ⁡ ( β z ) {\displaystyle \operatorname {sh} (i\beta z)=\sin(\beta z)}
9. Это свойство короткозамкнутого четвертьволнового отрезка линии позволяет использовать его в практических устройствах как «металлический изолятор».
10. Закон Ома

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 21 июня 2018 года.

>Это интересно!

22 декабря

Передача сигналов по витой паре

В

итая пара — это два скрученных провода в изоляции. Скручивание делается для того, чтобы оба провода находились в одинаковых условиях, то есть воздействие на них внешних помех не отличалось. В одном кабеле может быть несколько пар, обычно 2 или 4, заключенных в общую диэлектрическую оболочку. Информационный сигнал содержится в разности напряжений между проводами одной пары.
Существует несколько разновидностей витых пар:
– UTP (Unscreened Twisted Pair) — неэкранированная витая пара.
– FTP (Foiled Twisted Pair) — фольгированная витая пара с одним общим внешним экраном.
– SFTP (Shielded Foiled Twisted Pair) — фольгированная экранированная витая пара с двумя внешними экранами.
– STP (Shielded Twisted Pair) — защищенная витая пара. В таком кабеле каждая пара экранирована отдельным экраном.
– S/STP (Screened Shielded Twisted Pair) — защищенная экранированная витая пара, отличающаяся от STP наличием дополнительного общего внешнего экрана.
Одним из недостатков витой пары является возможность перехвата передаваемой информации. Это делается либо с помощью воткнутых в кабель двух иголок, либо путем считывания излучаемого кабелем электромагнитного поля. Экранирование обеспечивает защиту от электромагнитных наводок и несанкционированного подслушивания. С другой стороны, экранированный кабель значительно дороже, поэтому используется реже.
Кабели на основе витой пары по рабочей частоте делятся на следующие категории.
– К категории 1 относят обычные не витые телефонные кабели. По ним можно передавать только речь.
– Кабель категории 2 позволяет передавать данные в полосе частот до 1 МГц (используется редко).
– Кабель категории 3 используется для передачи данных в полосе частот до 16 МГц. Он состоит из витых пар с девятью витками проводов на 1 м длины.
– Кабель категории 4 передает данные в полосе частот до 20 МГц. Используется редко, т.к. не слишком отличается от категории 3. Стандартом рекомендуется вместо кабеля категории 3 переходить сразу на кабель категории 5.
– Кабель категории 5 в настоящее время самый совершенный кабель, рассчитанный на передачу данных в полосе частот до 100 МГц. Состоит из витых пар, имеющих не менее 27-ми витков на 1 м длины.
– Кабель категории 6 — перспективный тип кабеля для передачи данных в полосе частот до 200 (или 250) МГц.
– Кабель категории 7 — перспективный тип кабеля для передачи данных в полосе частот до 600 МГц.
Согласно стандарту EIA/TIA 568 (Американский стандарт кабельных систем, принятый в июле 1991 г.), полное волновое сопротивление кабелей категорий 3, 4 и 5 должно составлять 100 Ом ±15% в частотном диапазоне от 1 МГц до максимальной частоты кабеля. Волновое сопротивление экранированной витой пары STP равно 150 Ом ±15%.
Стандарт определяет также максимально допустимую величину рабочей емкости каждой из витых пар кабелей категории 4 и 5. Она должна составлять не более 17 нФ на 305 м при частоте сигнала 1 кГц и температуре окружающей среды 20°С.
Итак, преимущество витых пар заключается в простоте монтажа и ремонта, а также в низкой стоимости кабеля. С другой стороны, неэкранированные кабели на основе витых пар обладают рядом недостатков: они подвержены влиянию электромагнитных помех и не гарантируют защиту передаваемой информации. Максимальная длина кабеля составляет 100 м.

Характеристики

Основными электрическими характеристиками витой пары являются волновое сопротивление, затухание на 1 м длины и скорость распространения сигнала. Рассмотрим их подробнее.
1. Затухание (attenuation) — это величина, характеризующая потерю мощности сигнала при передаче. Коэффициент затухания вычисляется как отношение мощности полученного на конце линии сигнала к мощности сигнала, поданного в линию, и измеряется в децибелах на единицу длины. Затухания обусловлены потерями в диэлектрике и скин-эффектом. По сравнению с другими типами кабелей витая пара обладает самым большим коэффициентом затухания на данной частоте. Именно затухание сигнала ограничивает длину кабеля. Для увеличения длины канала связи следует использовать более качественные кабели с защитой от помех и наводок. Для уменьшения коэффициента затухания применяются специальные корректоры или сигнальные буферы со встроенной коррекцией предыскажений.
Предыскажения вносятся для того, чтобы сделать АЧХ более ровной. При этом нелинейные искажения сигнала уменьшаются. В усилительный тракт передатчика включается корректор — нелинейное устройство, передаточные характеристики которого подбираются так, чтобы амплитудная характеристика объединенного устройства корректор-усилитель стала линейной, а амплитудно-фазовая характеристика — равномерной.
Для чего это требуется? В линиях передачи с ровной АЧХ отсутствует межсимвольная интерференция, что повышает качество передачи. Чем выше подъем АЧХ, тем большие затухания компенсируются и больше максимальная длина линии.
Существуют корректоры трех типов. АЧХ постоянного амплитудного корректора не меняется. Такие корректоры используются в сетях с фиксированной длиной среды передачи. Переменный амплитудный корректор, наоборот, имеет несколько предустановленных настроек, которые можно изменять в соответствии с длиной канала связи. Наиболее удобные в использовании — адаптивные корректоры, которые автоматически определяют уровень потерь в среде передачи и подбирают оптимальные параметры корректирующих импульсов. Адаптивные корректоры обычно разрабатываются под конкретные среды передачи, поэтому при выборе устройства необходимо удостовериться, что оно рассчитано именно на тот тип линии передачи и те параметры, которые используются в сети.
При коррекции сильных затуханий нельзя забывать о системном шуме. Дело в том, что сигналы с компенсацией потерь 40 дБ становятся очень чувствительными к шуму. Действительно, если отношение сигнал/шум поддерживается на уровне 10—15 дБ, то шумы в линии передачи не должны превышать 50—55 дБ, иначе сигнал потеряется.
2. NVP (Nominal Velocity of Propa­gation) — скорость распространения сигнала в линии, которая выражается как отношение скорости распространения сигнала к скорости света.
3. NEXT (Near End CrossTalk) — переходное затухание, или перекрестные наводки на ближнем конце. Оно характеризует влияние соседних витых пар друг на друга и рассматривается только при двухсторонней передаче информации. Данный эффект проиллюстрирован на рис. 1. Сигнал, передаваемый по верхней витой паре, наводит помеху на нижнюю. При одностороннем обмене в расчет принимается параметр FEXT (Far End CrossTalk), характеризующий взаимодействие пар на дальнем конце. Для ослабления наводок применяется фольгирование.
4. Временная задержка распространения сигнала между двумя парами в кабеле (Pair-to-Pair Skew). Она появляется из-за того, что пары не идеально одинаковы, одна из них обязательно длиннее другой, поэтому сигнал проходит по ней больший путь. Типичное значение задержки составляет порядка 25 нс/100 м, но может доходить и до 45 нс/100 м. Этот параметр учитывается при скоростях передачи 100 Мбит/с и выше.
5. Временная задержка распространения сигнала внутри одной пары (Intra-Pair Skew). Она возникает в случае, если длины проводников в паре не совпадают. Обратимся к рис. 2. Пусть сигнал передатчика является парафазным. Видно, что из-за разной длины проводов на выходе появляется синфазная составляющая, при этом амплитуда полезного дифференциального сигнала уменьшается. Проблема осложняется тем, что для витой пары задержка распространения сигнала зависит от частоты, т.е. при передаче несинусоидального сигнала все компоненты задерживаются на разное время.

>Рис. 1. Перекрестные помехи в кабеле на основе витой пары

Рис. 2. Появление синфазной составляющей на выходе пары проводов с разной длиной

Рассмотрим некоторые заблуждения, относящиеся к временной задержке между проводниками в паре.
Миф 1: временная задержка распространения сигнала внутри одной пары не зависит от частоты. На самом деле в несвязанных парах, например в двойном коаксиальном кабеле, временная задержка постоянна и не зависит от частоты сигнала. Однако в случае STP и твинаксиального кабеля это не соблюдается (см. рис. 3).
Миф 2: временная задержка пропорциональна длине кабеля. Это утверждение верно только на очень низких частотах, когда длина волны сравнима с длиной кабеля. На рис. 3 видно, что в диапазоне 300…1500 МГц наибольшая временная задержка наблюдается в самом коротком кабеле.
Миф 3: временную задержку можно определить методом прямого измерения, т.е. на один конец пары подать дифференциальный сигнал, а на другом засечь интервал между моментами появления сигналов в каждом проводе. Как показывает практика, этот способ применим только для низких частот, поскольку концы кабеля являются фильтрами НЧ.

Рис. 3. Задержка сигнала между двумя проводами твинаксиального кабеля

Любая асимметрия в кабеле, в т.ч. и разность задержек сигнала внутри пары, приводит к появлению синфазной составляющей сигнала. При этом амплитуда дифференциальной составляющей уменьшается. Неприятность заключается в том, что дифференциальные и синфазные сигналы имеют различную скорость распространения и различные коэффициенты потерь, поэтому при переходе энергии из одной формы в другую фаза и частота сигнала могут меняться непредсказуемым образом, приводя к возникновению фазового дрожания (джиттера). Заметим, что сами по себе синфазные составляющие не вносят дрожание в дифференциальный сигнал. Однако преобразование составляющих из одной формы в другую существенно портят сигнал. Если дрожание мало или полностью отсутствует, то схема приемника значительно упрощается. Именно поэтому важно контролировать временные задержки в линиях связи и применять меры для их минимизации.
На практике фазовое дрожание определяют по амплитуде синфазной и дифференциальной составляющих, а точнее исходя из их отношения. Для проведения необходимых измерений требуется сетевой анализатор. Этот прибор очень дорогой и его обычно заменяют более простым устройством, схема которого приведена на рис. 4. Оно состоит из двух соединителей H9-SMA, работающих на частотах 2 МГц — 2 ГГц. Один из них нужен для генерации дифференциального сигнала (верхний на рисунке), второй — для отделения дифференциальной составляющей от синфазной. Далее сигналы поступают на измеритель мощности, который определяет их величину. По этим данным вычисляется фазовое дрожание.