Понятие «электрического размера» — Часть 1

Один из важных параметров для понимания сути явлений и процессов, происходящих в печатной плате и в аппаратуре в целом, — «электрический размер» . Печатную плату в общем виде можно рассматривать как некоторую излучающую электромагнитную структуру. Будем считать, что излучающая электромагнитная структура — это любая структура, состоящая из проводников, проводящих ток. «Электрический размер» наиболее важен в определении эффективности электромагнитной связи структуры с другими объектами.

Электрические размеры измеряют в длинах волны. Длина волны – это расстояние, которое электромагн. волна должна пройти для того, чтобы фаза сдвинулась на 360°. В общем, это имеет отношение к одному из типов волны: однородной плоской волне. Свойство сдвига по фазе также связано с временем распространения волны между 2-мя точками. Достаточно будет просто определить электрические размеры платы или другой электромагнитной структуры в терминах длин волн. Длины волн обозначаются символом К. Для начала предположим, что электромагнитные волны распространяются в среде без потерь. В этом случае длина волны может быть рассчитана по известной формуле:

λ = v/f, (7.1)

Где v — скорость распространения электромагнитной волны в данной среде; f— частота синусоидального колебания.

При импульсном сигнале частота определяется как максимальная частота спектра сигнала, что определяет минимальную длину волны.

Электрический размер некоторой структуры в длинах волн можно выразить следующим образом:

База знаний ICS

Только физическая длина кабеля. Регистрируется по нанесенным на внешнюю оболочку кабеля футовым/двухфутовым (американский стандарт) или метровым (европейский стандарт) меткам. Правила нанесения меток однозначно оговорены в соответствующих стандартах. Физическая длина кабеля является как техническим (соответствие требованиям стандартов), так и «юридическим» (сертификация и регистрация системы при предоставлении гарантии) критерием. Согласно TSB67 – «Физическая длина Базовой линии / Канала определяется как сумма физических длин кабелей, находящихся между двумя конечными точками. Физическая длина Базовой линии / Канала может быть установлена с помощью физического измерения длины кабеля/кабелей, определена по меткам длины, нанесенным на кабель (если имеются), или оценена на основании измерений электрической длины». Измеренная электрическая «длина» кабеля – это всего лишь верификационный параметр, позволяющий исключить ошибки монтажа и удостовериться в том, что путь прохождения сигнала укладывается в допустимые пределы. Не рекомендуется ссылаться на измеренную электрическую длину кабеля в вопросах касающихся учета длины израсходованного кабеля и в любых других вопросах, связанных с механическими параметрами системы.

Требования к тестированию длины (TSB67):

• Максимальная физическая длина Базовой линии должна составлять 94 м (включая тестовые шнуры)
• Максимальная физическая длина Канала должна составлять 100 м (включая аппаратные шнуры и кроссировочные перемычки / патч-шнуры)

Погрешности при измерении длины кабеля (пары) следующие (TSB67):

• Полевые тестеры классов Level I и Level II: +/- 1 м +/- 4%
• Поправка на неопределенность NVP: +10% (с точки зрения чистой физики неопределенность NVP должна выражаться в форме диапазона +/- 10%, но «-» опускается, так как при этом результаты и так заведомо попадут в допустимые стандартами пределы).

Таким образом, при тестировании Базовой линии с предельной длиной 90 м (в соответствии с ISO/IEC 11801, EN 50173, AS/NZS 3080 или ANSI/TIA/EIA-568-A) полная предельная длина тестируемого сегмента составит 94 м (TSB67) с учетом 2 м тестовых шнуров на каждом концы линии, и предел измерения полевого тестера при определении критерия PASS/FAIL составит 90+4+10%=103.4 м. Кроме того, учтите собственную погрешность полевого тестера (+/- 1 м или +/- 4%, в зависимости от того, что больше), и вы получите диапазон вероятных результатов: от 98.3 м до 108.4 м. Тестер обо всем этом «знает», и в результате вы получите четыре возможных критерия – PASS, PASS*, FAIL*, FAIL. Результаты, помеченные звездочкой * – это те значения, которые оказались в области погрешностей полевого тестера, и однозначно их интерпретировать невозможно. В качестве конечного результата тестирования регистрируется измеренная электрическая длина самой короткой из всех пар, входящих в кабельный узел. Если пойти дальше и учесть и этот фактор, то разница между самой длинной и самой короткой парами может составить для Базовой линии длиной 90 м (при требовании к смещению задержки в 40 нс для Базовой линии – ANSI/TIA/EIA-568A-1): L = c x DelaySkew = 300 000 000 м/с х 0.0000000040 с = 12 м. У реальных кабелей хорошего качества смещение задержки, как правило, не выходит за рамки 35 нс на 100 м у кабелей Категории 5е (Класс D PDAM 3) и 25 нс на 100 м у кабелей Категорий 6 и 7 (Классы E и F). Как видите, тестирование электрической длины кабеля (пары) не может заменить собой измерение физической длины кабеля.

Примечание: все приведенные расчеты и результаты являются экстремальными, в реальной практике их получение маловероятно, и приведены они только в качестве примера, иллюстрирующего концепцию полевого тестирования электрической длины кабелей.

Тема 17. Линии передачи Т-волны

Коаксиальная линия. Структура ЭМП Т-волны, волновое сопротивление, переносимая мощность. Структура токов на внешнем и внутреннем проводниках. Ослабление. Высшие типы волн. Условие одноволнового режима работы. Электрическая и тепловая прочность. Критерии выбора волнового сопротивления. Область применения коаксиальных волноводов.

Симметричная двухпроводная линия передачи. Структура ЭМП, волновое сопротивление. Распределение токов по сечению проводников. Выбор размеров поперечного сечения линии. Коэффициент ослабления. Электрическая и тепловая прочность. Экранированные двухпроводные линии.

Линии типа «витая пара». Область применения двухпроводных линий.

Полосковые линии передачи и их разновидности. Симметричные и несимметричные полосковые линии. Структура поля основной волны. Основные характеристики полосковых линий. Волновое сопротивление. Выбор размеров поперечного сечения. Микрополосковые линии. Щелевая и компланарная полосковые линии: структура поля основной волны. Электрическая и тепловая прочность полосковых линий. Область применения полосковых линий.

Указания к теме

В результате изучения этой темы необходимо усвоить особенности конструкций и параметров передающих линий Т-волны основных типов, а также подходы к расчету их электрических характеристик.

При изучении направляющих систем с Т-волной следует обратить внимание на особенности, отличающие их от односвязных волноводов, провести сравнение по таким параметрам, как ширина рабочей полосы частот, уровень потерь, электрическая прочность, габариты, дисперсия, знать область применения. Необходимо научиться рассчитывать погонные параметры линии, сводить определенную линию передачи Т-волны к обобщенному эквиваленту.

Следует уяснить критерии выбора волнового сопротивления коаксиального кабеля 30, 50, 75 Ом для различных радиотехнических задач.

Основные сведения

Направляющие системы в виде линии передачи Т-волны широко применяются в радиотехнике в диапазоне от низких частот и до СВЧ. Данные ЛП обладают малой дисперсией и малым затуханием в диапазонах ВЧ–УВЧ.

К двухсвязным ЛП Т-волны относятся коаксиальная, двухпроводная и различные виды полосковых линий. Для анализа распространения ЭМВ в таких ЛП применяют обобщенную модель, в которой элементарный отрезок линии заменяется эквивалентом из элементов с сосредоточенными параметрами (рис. 17.1) . Данный подход основан на свойствах Т-волны при отсутствии волн высших типов и дает достаточную точность, если поперечные размеры ЛП << l, а конфигурация проводников такова, что по одному проводнику ток от генератора поступает к нагрузке, а по другому возвращается обратно к генератору.

Элементы схемы (рис. 17.1) имеют такие значения: R0 –сопротивление проводников линии; G0 –проводимость диэлектрика линии; L0 и C0 – индуктивность и емкость линии, – и называются погонными параметрами линии.

Поперечное сечение коаксиальной линии передачи (КЛ) показано на рис. 17.2 (а – радиус внутреннего проводника; b – внешнего). Внешний проводник КЛ одновременно является экраном, поэтому все ЭМП сосредоточено внутри линии в пространстве между проводниками.

Внутренний проводник имеет меньшую площадь поперечного сечения, чем внешний, и является основным источником потерь КЛ. Кроме того, пробой линии также может произойти около внутреннего проводника, так как напряженность поля в этом месте максимальна. Низшую критическую частоту из мод высших порядков имеет H11 (lкр=p(a+b)), обычно эта частота находится в СВЧ диапазоне, рабочая частота выбирается намного ниже критической, так как затухание КЛ в СВЧ диапазоне становится значительным .

Для повышения гибкости КЛ внутренний проводник не имеет жесткого крепления с диэлектриком, а внешний проводник выполняется в виде оплетки.

Поперечное сечение двухпроводной линии (ДЛ) показано на рис. 17.3 (а – радиус проводника, D – расстояние между осями проводников). Хотя данная линия является открытой, при выполнении условия квазистационарности считается, что все ЭМП ДЛ сконцентрировано вокруг линии внутри окружности радиусом 5D . Однако на ВЧ и выше ДЛ начинает заметно излучать, так как внешние ЭМП, создаваемые противоположно направленными токами в проводах, компенсируются не полностью.

При малых расстояниях между проводниками проявляется эффект близости, который заключается в появлении асимметрии в распределении тока по сечениям проводников, что увеличивает затухание ДЛ.

При D/a > 8 эффектом близости можно пренебречь.

Проводники ДЛ одинаковы, поэтому при аналогичных с КЛ размерах затухание в проводниках линии будет меньше.

Для повышения рабочей частоты проводники ДЛ скручивают (такая ЛП называется также витой парой). Устранить излучение из ДЛ можно с помощью экранирования, но экранированная ДЛ относится к многосвязным ЛП.

При конструировании устройств УВЧ и СВЧ КЛ находят ограниченное применение как соединительные линии и линии задержки. В устройствах указанных диапазонов удобнее применять полосковые и особенно микрополосковые линии, что позволяет существенно уменьшить размеры устройств и создавать интегрированные конструкции.

На рис. 17.4 и 17.5 приведены поперечные сечения симметричной полосковой (СПЛ) и микрополосковой (МПЛ) линий соответственно.

Конструктивные параметры СПЛ:

h – толщина центрального проводника;

w – ширина центрального проводника;

b – расстояние между пластинами;

e – диэлектрическая проницаемость.

Аналогично для МПЛ:

h – толщина центрального проводника;

w – ширина центрального проводника;

b – толщина диэлектрической подложки;

e – диэлектрическая проницаемость по­д­ложки; e¢ – диэлектрическая проницаемость неограниченно простирающейся среды над подложкой и центральным проводником.

МПЛ завоевали популярность при конструировании микроэлектронных УВЧ и СВЧ устройств из-за конструктивной простоты и удобства монтажа элементов. Отсутствие симметрии и распространение ЭМВ в разных средах существенно усложняют анализ и заставляют считаться с частотной дисперсией. Для минимизации дисперсии в изготовляемом устройстве применяют заполнение диэлектриком верхнего над малым проводником пространства, что делает похожей структуру ЭМП в МПЛ на структуру ЭМП в СПЛ.

Более подробные сведения о линиях передачи Т-волны и формулы для расчета их характеристик можно найти в рекомендуемой литературе.

Телеграфные уравнения.В линиях передачи Т-волны возможен переход от векторных величин 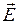и 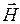к скалярным величинам U (напряжение между проводниками 1 и 2) и I (ток):

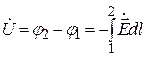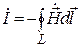; , (17.1)

где L – замкнутый контур, охватывающий проводник с током .

Уравнения Максвелла для линий передачи с Т-волной сводятся к известным из теории цепей телеграфным уравнениям:

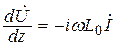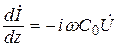; . (17.2)

Волновые уравнения для напряжения и тока.От уравнений (17.2) можно перейти к волновым уравнениям для напряжения и тока:

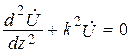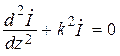; , (17.3)

где волновое число при отсутствии потерь .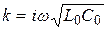

Характеристическое сопротивление ЛП с малыми потерями

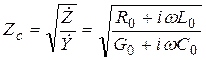. (17.4)

Для учета потерь в диэлектриках и проводниках линии передачи в уравнение (17.2) вводят комплексные сопротивление и проводимость

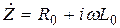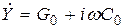; . (17.5)

В этом случае (17.2) запишется в виде

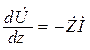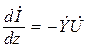; , (17.6)

а волновое число .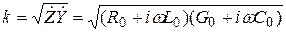

Характеристическое сопротивление линии передачи с учетом потерь (17.5) определяется формулой

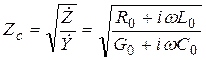. (17.7)

В линии без потерь (R0 = 0, G0 = 0)

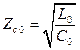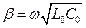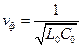; ; . (17.8)

Решением волновых уравнений (17.3) для напряжения и тока являются соответственно прямые и обратные волны напряжения и тока, аналогичные (7.8):

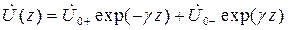; (17.9)

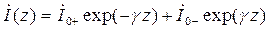. (17.10)

Для линий передачи Т-волны можно связать L0, С0 и Zc0 так :

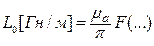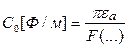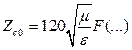, , , (17.11)

где F(…) – функция, связанная с геометрическими размерами линии.

Характеристики КЛ определяются по формулам :

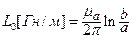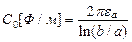; ; (17.12)

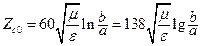; (17.13)

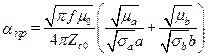; (17.14)

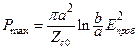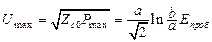; , (17.15)

где Eпроб – пробивная напряженность диэлектрика КЛ; Umax – максимально допустимое напряжение в КЛ; Pmax – предельно допустимая мощность в КЛ.

Анализ (17.12)–(17.15) позволил найти соотношения конструктивных параметров для достижения оптимальных характеристик .

Минимум затуханиядостигается при b/a = 3,6…5,6, Zc0 = (77…103)/ 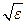,что соответствует стандартному значению Zc0 = 75 Ом.

Максимум напряжения пробоя КЛ достигается при b/a = 2,72, Zc0 = 60/ 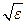, что соответствует стандартному значению Zc0 = 50 Ом.

Максимум передаваемой мощности достигается при b/a=1,65, Zc0 = 30/ 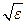, что соответствует Zc0 = 30 Ом. В данное время КЛ с Zc0 = 30 Ом применяется достаточно редко.

КЛ с Zc0 = 75 Ом применяется в приемной технике УКВ диапазона (соединение приемника телевещания или радиовещания с антенной), а с Zc0 = 50 Ом – в связной технике (передача, прием-передача).

Характеристики ДЛ (m1 – m диэлектрика, а m2 – m проводников):

;

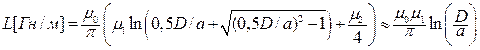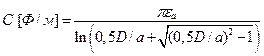
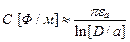. (17.16)

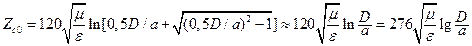. (17.17)

Приближенные формулы можно использовать при значительном расстоянии между проводниками ДЛ (D/a > 6).

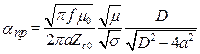; (17.18)

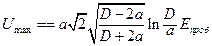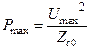; . (17.19)

Точные методы расчета характеристик СПЛ и МПЛ содержат сложные и неявно заданные формулы, аппроксимация которых привела к существованию разнообразных формул разной степени точности. Для оценочных расчетов характеристик СПЛ и МПЛ рекомендуется применять простейшие формулы .

Характеристики СПЛ определяются формулами

при w/(b–h) < 1 ;

при w/(b–h) > 1 ; (17.20)

;

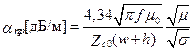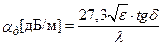. (17.21)

На рис. 17.6 приведен график зависимости ZcСПЛ от w/b приh/b = 0,01 и e = 1, построенный по формулам (17.20). Сравнение с точными значениями показывает, что погрешность (17.20) в данном случае не превышает ± 5 % .

Характеристики МПЛ определяются формулами

при w/b < 2;

при w/b ³ 2; (17.22)

; ;

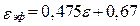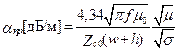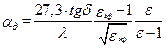. (17.23)

На рис. 17.7 приведены графики зависимости ZcМПЛ от w/b приh/b = 0,01 и e = 3,8, построенные по формулам (17.22) и точным значениям из . Анализ показывает, что погрешность (17.22) в данном случае не превышает 20 % .

Оценка дисперсии в ЛП Т-волны проводится в предположении малости потерь, что позволяет разделить потери в проводнике и потери в диэлектрике. Появление потерь вызывает появление продольных составляющих ЭМВ, но при малых потерях отличие ЭМП от ЭМП Т-волны пренебрежимо мало .

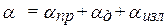, (17.24)

где 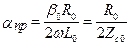; ; 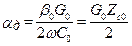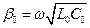, в закрытых ЛП aизл = 0.

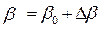, (17.25)

где 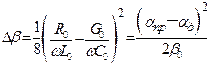– дисперсионная добавка коэффициента фазы.

Кроме изменения a и b, групповой и фазовой скоростей, потери вызывают частотную зависимость характеристического сопротивления

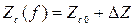, (17.26)

где 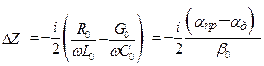– дисперсионная добавка .

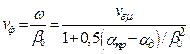. (17.27)

Активная проводимость утечки в изоляции G0 определяется так :

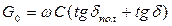. (17.28)

Из (10.15) с помощью формулы (10.12) находим составляющую коэффициента затухания, определяемую потерями в диэлектрике:

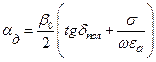. (17.29)

Полученное равенство справедливо для любого типа линий. Для любых технических диэлектриков на ВЧ и выше можно пренебречь вторым слагаемым в скобках по сравнению с первым. Величина 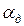растет пропорционально частоте.

Скин-эффект в проводниках приводит к появлению реактивной составляющей, что требует замены R0 на Z0 = R0 +iX0 . На ВЧ и выше Z0 (f) определяется так:

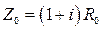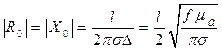, . (17.30)

В линиях с малыми потерями отличие vф от vem и Zc от Zc0 мало.

Из (17.25) – (17.27) видно, что при выполнении условия 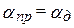дисперсионные искажения отсутствуют, и условие неискаженной передачи через первичные параметры записывается так:

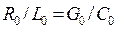. (17.31)

В прошлом, когда сообщения по линиям связи передавались на дальние расстояния на НЧ, особое значение придавали выполнению условия (17.31), для чего искусственно увеличивали индуктивность ЛП. В настоящее время это не требуется, так как потери в диэлектриках ЛП малы.

Условие неискаженной передачи с учетом (17.29) – (17.31) выполняется на некоторой частоте ОВЧ-СВЧ диапазонов, которая зависит от параметров линии. На рис. 17.8 приведены частотные зависимости составляющих затухания.

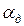~f ; 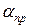постоянно на низких частотах, а на более высоких ~f 0,5. Следовательно, на НЧ 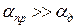, 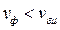и растет с частотой. Потери в проводниках линии вызывают ано­маль­ную дисперсию ЭМВ.

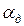растет с частотой быстрее, чем 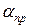, и некоторой частоте fнп в диапазоне ОВЧ-СВЧ достигается условие неискаженной передачи. 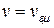; 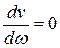, групповая скорость постоянна, и дисперсионных искажений нет.

При f > fнп 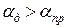, наблюдается нормальная дисперсия. Из-за большой величины b изменение v(f) и других параметров настолько невелико, что дисперсией пренебрегают .

Таким образом, дисперсию ЭМВ в линиях передачи Т-волны и комплексный характер Zc обычно учитывают только на НЧ.

В диапазонах УВЧ и СВЧ при анализе распространения относительно узкополосных сигналов влиянием дисперсии можно пренебречь.

Наибольшую дисперсию имеют МПЛ :

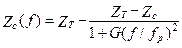, (17.32)

где 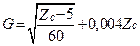, , 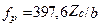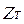– Zc СПЛ шириной w и высотой 2b.

Однако в любой октаве рассматриваемых диапазонов относительные изменения вторичных параметров МПЛ не превышают 1%.

Список рекомендуемой литературы:.

Контрольные вопросы и задания

1. Опишите конструкции основных линий передачи Т-волны.

2. Запишите формулы для вычисления волнового сопротивления линий передачи Т-волны основных типов.

3. Опишите распределение ЭМП в пространстве линий передачи Т-волны.

4. Поясните физический смысл понятий тока и напряжения в линиях передачи Т-волны.

5. Дайте сравнительную характеристику параметров коаксиальной и двухпроводной линий.

6. Какие достоинства имеет двухпроводная линия в виде «витой пары»?

7. Назовите основные разновидности полосковых линий.

8. Дайте сравнительную характеристику СПЛ и МПЛ.

9. Какие особенности имеют многосвязные линии?

10. Какое влияние оказывает синфазность или противофазность возбуждения проводников связанных линий?

11. Укажите основные разновидности и область применения многосвязных ЛП.

12. Чем отличается Т-волна от квази-Т-волны?

13. По каким критериям выбирают Zc коаксиальных линий?

14. Для каких радиотехнических целей используются коаксиальные кабели с характеристическим сопротивлением 50 и 75 Ом?

	|	следующая лекция ==>
Волноводы сложных форм сечения	|	Тема 18. Волоконные световоды и другие Линии передачи

Дата добавления: 2018-09-24; просмотров: 199;

>Волновое сопротивление

Волновое сопротивление — характеристика среды распространения волны.

В электродинамике

В электродинамике волновое сопротивление линии передачи (коротко — волновое сопротивление) — величина, определяемая отношением напряжения падающей волны к току этой волны в линии передачи (по закону Ома).

При определении волнового сопротивления может использоваться также напряжение и ток отражённой или бегущей волн.

Единица измерения — Ом.

При расчёте волнового сопротивления по методу комплексных амплитуд используют амплитуды напряжения и силы тока. При наличии потерь в линии передачи значение становится комплексным.

Волновое сопротивление линии передачи зависит от её конструкции и электрофизических параметров применяемых материалов (ε, μ, σ), что совместно определяет погонные параметры линии передачи (ёмкость, индуктивность, сопротивление и проводимость на единицу длины), а также от типа волны, при наличии дисперсии — от частоты электромагнитных колебаний.

Волновое сопротивление часто путают с характеристическим сопротивлением волны — величиной, определяемой отношением поперечной составляющей напряженности электрического поля к поперечной составляющей напряженности магнитного поля бегущей волны.

В длинной линии волновое сопротивление равно (по закону Ома):

Z 0 = U m I m , {\displaystyle Z_{0}={U_{m} \over I_{m}},}

где:

• U m {\displaystyle U_{m}} — амплитуда напряжения волны (падающей, отраженной или бегущей);
• I m {\displaystyle I_{m}} — амплитуда силы тока той же волны.

В бесконечно длинных линиях нагрузка имеет чисто активный характер, поэтому энергия, запасаемая в индуктивности и ёмкости, одинаковая.

L 1 X I m 2 2 = C 1 X U m 2 2 , {\displaystyle {L_{1}XI_{m}^{2} \over 2}={C_{1}XU_{m}^{2} \over 2},}

где:

• L 1 {\displaystyle L_{1}} — погонная индуктивность;
• C 1 {\displaystyle C_{1}} — погонная ёмкость;
• X {\displaystyle X} — часть линии;
• U m {\displaystyle U_{m}} — амплитуда напряжения в линии;
• I m {\displaystyle I_{m}} — амплитуда силы тока в линии.

Поэтому волновое сопротивление в бесконечно длинных линиях определяется погонными индуктивностью и ёмкостью:

L 1 C 1 = U m I m = Z 0 . {\displaystyle {\sqrt {L_{1} \over C_{1}}}={U_{m} \over I_{m}}=Z_{0}.}

Волновое сопротивление среды — отношение амплитуд электрического и магнитного полей электромагнитных волн, распространяющихся в среде:

Z = E 0 − ( x ) H 0 − ( x ) . {\displaystyle Z={E_{0}^{-}(x) \over H_{0}^{-}(x)}.}

Если волновые сопротивления двух сред, имеющих границу раздела, одинаковы, то на этой границе не происходит отражения электромагнитных волн, даже если диэлектрическая и магнитная проницаемости в средах различны.

Определение параметров коаксиального кабеля

Одним из основных параметров высокочастотного кабеля является волновое сопротивление. Обычным омметром его не измерить — для этого нужен специальный прибор. Сам кабель (отечественного производства) не имеет маркировки и если вы не знаете его тип, то, воспользовавшись штангенциркулем, легко сможете определить волновое сопротивление с помощью несложных вычислений.

Для этого нужно снять внешнюю защитную оболочку с конца кабеля, завернуть оплетку и измерить диаметр внутренней полиэтиленовой изоляции. Затем снять изоляцию и измерить диаметр центральной жилы. После этого результат первого измерения разделим на результат второго: при полученном отношении примерно 3, 3…3, 7 волновое сопротивление кабеля составит 50 Ом, при отношении 6, 5…6, 9 — составляет 75 Ом.

Вторым важным параметром является удельное затухание. Эта величина характеризует потери уровня сигнала при его прохождении через один метр кабеля и позволяет сравнивать кабели разных марок.

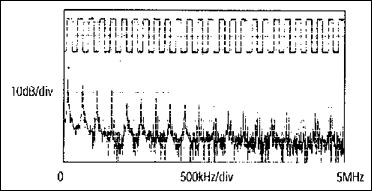
Затухание тем больше, чем больше длина кабеля и чем больше частота сигнала. Удельное затухание измеряется в децибелах на метр (дБ/м) и приводится в справочниках в виде таблиц или графиков.

На рисунке приведены зависимости удельного затухания коаксиальных кабелей разных марок от частоты. Пользуясь ими, можно подсчитать затухание сигнала в кабеле, при известной его длине, на любой частоте.

Обозначение коаксиального кабеля состоит из букв и трех чисел: буквы РК обозначают радиочастотный коаксиальный кабель, первое число показывает волновое сопротивление кабеля в омах, второе — округленный внутренний диаметр оплетки в миллиметрах, третье — номер разработки. Из графика видно, что удельное затухание зависит от толщины кабеля: чем он толще, тем удельное затухание меньше.

Зная длину кабеля, воспользовавшись таблицей, можно перевести затухание из децибелов в относительное ослабление уровня сигнала на выходе.

Для практического определения волнового сопротивления любой неизвестной линии передачи, от коаксиального кабеля до пары скрученных проводов, можно также воспользоваться измерителем индуктивности и емкости.

Волновое сопротивление линии с малыми потерями определяется по формуле:

, где

Z — волновое сопротивление (Ом); L — индуктивность закороченной линии (Гн); С — емкость разомкнутой линии (Ф).

Для расчета необходимо выполнить измерение индуктивности закороченного куска линии длиной 1…5 м, а затем измерить емкость разомкнутого на конце куска. При меньшей или большей длине отрезка линии погрешность измерения увеличивается.

Например, волновое сопротивление сетевых шнуров питания лежит в пределах 30…60 Ом, большинства экранированных микрофонных шнуров — 40…70 Ом, телефонной пары — 70…100 Ом.