Почему мы занимаемся кодами Рида-Соломона

Одно из главных направлений работы компании YADRO — разработка систем хранения данных (СХД). Можно долго обсуждать, какие характеристики данных систем являются самыми важными с точки зрения конечного пользователя. Это может быть скорость операций ввода/вывода, стоимость владения системой, уровень энергопотребления или что-то ещё. Но все эти характеристики будут иметь смысл только в том случае, если система обеспечивает необходимый пользователю уровень сохранности данных. Как результат, для всех разработчиков подобных систем, вопросы обеспечения надёжности хранения данных выходят на первый план.
Долгое время главным игроком в сфере безопасного хранения данных оставалась технология RAID. Подобные классические решения, наряду с известными плюсами, обладают и определёнными ограничениями. К ним можно отнести:

• относительно низкий уровень защиты (например, RAID 6 поддерживает выход из строя максимум двух дисков)
• необходимость держать запасные диски
• невозможность контролировать распределение «parity» блоков (это может быть важно для определенных типов дисков)
• сложность поддержки «гетерогенных» дисков

В связи с этим, в последнее время, набирают популярность технологии, основанные на всевозможных избыточных кодах (в англоязычной литературе за подобными технологиями закрепилось название — erasure coding), которые предоставляют гораздо больше возможностей по сравнению с классическим RAID.
На данный момент наша команда занимается разработкой системы хранения данных TATLIN. По архитектуре системы мы планируем написать отдельную серию статей, тут лишь скажем, что в какой-то момент времени перед нами встала задача реализации собственной системы надёжного хранения данных. После изучения вопроса мы решили остановиться на проверенных временем кодах Рида-Соломона. Существуют готовые библиотеки (например, ISA-L от Intel или Jerasure авторства James S. Plank). В них реализованы соответствующие процедуры кодирования/декодирования. Но учитывая, что наша аппаратная платформа построена на базе архитектуры OpenPOWER, а вся логика системы реализована как модуль ядра ОС Linux, — было принято решение делать свою реализацию, оптимизированную под особенности нашей системы.
В этой первой статье я попытаюсь объяснить, о чем идет речь, когда говорят о кодах Рида-Соломона в контексте систем хранения данных. Начнем с простых примеров, которые позволят лучше уяснить сущность решаемых проблем.

Базовая задача восстановления утраченного

Предположим, что есть два произвольных целых числаи. Необходимо разработать алгоритм, который двум этим числам поставит в соответствие третье число, причём такое, что по нему будет возможно однозначно восстановить любое из двух исходных чисел при потере одного из них. Другими словами, имея пару (и) или (и), возможно однозначно восстановитьилисоответственно. Существует много вариантов реализации подобного алгоритма, но, вероятно, самым простым является тот, который к двум исходным числам применяет битовую операцию «Исключающее «ИЛИ» (XOR)», т.е.. Тогда для восстановленияможно воспользоваться равенством(для восстановления,).
Немного усложним задачу. Предположим, что исходных чисел не два, а три —,и. Как и прежде, нужен алгоритм, позволяющий справиться с потерей одного из исходных чисел. Легко заметить, что ничто не мешает снова использовать битовую операцию «Исключающее «ИЛИ»»,. Для восстановленияможно воспользоваться равенством.
Усложним задачу ещё немного. Как и прежде, имеется три числа,и, а вот потерять, в этот раз, мы можем не одно, а любые два из них. Очевидно, что просто использовать операцию «Исключающее «ИЛИ» уже не получится. Как же восстанавливать потерянные числа?

Принцип кодирования Рида-Соломона на простых примерах с картинками

Одним, из возможных путей решения данной задачи, является применение кодов Рида-Соломона. Формальное описание метода легко найти в Интернете, но основная проблема заключается в том, что людям, далеким от «полей Галуа», достаточно сложно понять, как, собственно, всё это работает. Вот, например, определение из Википедии:

Попробуем разобраться с тем, как это работает, начав с более интуитивных вещей. Для этого вернемся к нашей последней задаче. Напомним, что есть три произвольных целых числа, любые два из них могут быть потеряны, необходимо научиться восстанавливать потерянные числа по оставшимся. Для этого применим «алгебраический» подход.
Но прежде необходимо напомнить еще об одном важном моменте. Технологии восстановления данных неспроста называются методами избыточного кодирования. По исходным данным вычисляются некоторые «избыточные», которые потом позволяют восстановить потерянные. Не вдаваясь в подробности заметим, что эмпирическое правило такое — чем больше данных может быть потеряно, тем больше «избыточных» необходимо иметь. В нашем случае для восстановления двух чисел, нам придётся по некоторому алгоритму сконструировать два «избыточных». В общем случае, если нужно поддерживать потерючисел, необходимо соответственно иметьизбыточных.
Упомянутый выше «алгебраический» подход состоит в следующем. Составляется матрица специального вида размера. Первые три строки этой матрицы образуют единичную матрицу, а последние две — это некоторые числа, о выборе которых мы поговорим позднее. В англоязычной литературе эту матрицу обычно называют generator matrix, в русскоязычной встречается несколько названий, в этой статье будет использоваться — порождающая матрица. Умножим сконструированную матрицу на вектор, составленный из исходных чисел

,и.

В результате умножения матрицы на вектор с данными получаем два «избыточных» числа, обозначенных на рисунке каки. Давайте посмотрим, как с помощью этих «избыточных» данных можно восстановить, к примеру, потерянныеи.
Вычеркнем из порождающей матрицы строки, соответствующие «пропавшим» данным. В нашем случаесоответствует первой строке, а– второй. Полученную матрицу умножим на вектор с данными, и в результате получим следующее уравнение:

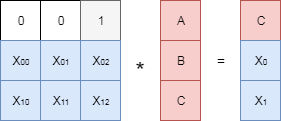
Проблема лишь в том, чтоимы потеряли, и они нам теперь неизвестны. Как мы можем их найти? Есть очень элегантное решение этой проблемы.
Вычеркнем соответствующие строки из порождающей матрицы и найдём обратную к ней. На рисунке эта обратная матрица обозначена как. Теперь домножим левую и правую части исходного уравнения на эту обратную матрицу:

Сокращая матрицы в левой части уравнения (произведение обратной и прямой матриц есть единичная матрица), и учитывая тот факт, что в правой части уравнения нет неизвестных параметров, получаем выражения для искомыхи.

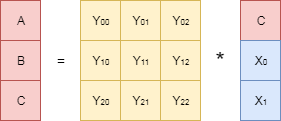
Собственно говоря, то, что мы сейчас проделали — основа всех типов кодов Рида-Соломона, применяемых в системах хранения данных. Процесс кодирования заключается в нахождении «избыточных» данных,, а процесс декодирования — в нахождении обратной матрицы и умножения её на вектор «сохранившихся» данных.
Нетрудно заметить, что рассмотренная схема может быть обобщена на произвольное количество «исходных» и «избыточных» данных. Другими словами, по исходнымчислам можно построитьизбыточных, причем всегда возможно восстановить потерю любыхизчисел. В этом случае порождающая матрица будет иметь размер, а верхняя часть матрицы размеромбудет единичной.
Вернемся к вопросу о построении порождающей матрицы. Можем ли мы выбрать числапроизвольным образом? Ответ – нет. Выбирать их нужно таким образом, чтобы вне зависимости от вычеркиваемых строк, матрица оставалась обратимой. К счастью, в математике давно известны типы матриц, обладающие нужным нам свойством. Например, матрица Коши. В этом случае сам метод кодирования часто называют методом Коши-Рида-Соломона (Cauchy-Reed-Solomon). Иногда, для этих же целей используют матрицу Вандермонда, и соответственно, метод носит название Вандермонда-Рида-Соломона (Vandermonde-Reed-Solomon).
Переходим к следующей проблеме. Для представления чисел в ЭВМ используется фиксированное число байтов. Соответственно, в наших алгоритмах мы не можем свободно оперировать произвольными рациональными, и тем более, вещественными числами. Мы просто не сможем реализовать такой алгоритм на ЭВМ. В нашем случае порождающая матрица состоит из целых чисел, но при обращении этой матрицы могут возникнуть рациональные числа, представлять которые в памяти ЭВМ проблематично. Вот мы и дошли до того места, когда на сцену выходят знаменитые поля Галуа.

Поля Галуа

Итак, что такое поля Галуа? Начнём опять с поясняющих примеров. Мы все привыкли оперировать (складывать, вычитать, умножать, делить и прочее) с числами – натуральными, рациональными, вещественными. Однако, вместо привычных чисел, мы можем начать рассматривать произвольные множества объектов (конечные и/или бесконечные) и вводить на этих множествах операции, аналогичные сложению, вычитанию и т.д. Собственно говоря, математические структуры типа групп, колец, полей — это множества, на которых введены определенные операции, причем, результаты этих операций снова принадлежат исходному множеству. Например, на множестве натуральных чисел, мы можем ввести стандартные операции сложения, вычитания и умножения. Результатом опять будет натуральное число. А вот с делением все хуже, при делении двух натуральных чисел результат может быть дробным числом.
Поле – это множество, на котором заданы операции сложения, вычитания, умножения и деления. Пример — поле рациональных чисел (дробей). Поле Галуа — конечное поле (множество, содержащее конечное количество элементов). Обычно поля Галуа обозначаются как, где— количество элементов в поле. Разработаны методы построения полей необходимой размерности (если это возможно). Конечным результатом подобных построений обычно являются таблицы сложения и умножения, которые двум элементам поля ставят в соответствие третий элемент поля.
Может возникнуть вопрос – как мы всё это будем использовать? При реализации алгоритмов на ЭВМ удобно работать с байтами. Наш алгоритм может принимать на входебайт исходных данных и вычислять по нимбайт избыточных. В одном байте может содержаться 256 различных значений, поэтому, мы можем создать полеи рассчитывать избыточныебайт, пользуясь арифметикой полей Галуа. Сам подход к кодированию/декодированию данных (построение порождающей матрицы, обращение матрицы, умножение матрицы на столбец) остаётся таким же, как и прежде.
Хорошо, мы в итоге научились по исходнымбайтам конструировать дополнительныебайт, которые можно использовать при сбоях. Как это всё работает в реальных системах хранения? В реальных СХД обычно работают с блоками данных фиксированного размера (в разных системах этот размер варьируется от десятков мегабайт до гигабайтов). Этот фиксированный блок разбивается нафрагментов и по ним конструируются дополнительныефрагментов.
Процесс конструирования фрагментов происходит следующим образом. Берут по одному байту из каждого изисходных фрагментов по смещению 0. По этим данным генерируется K дополнительных байтов, каждый из который идет в соответствующие дополнительные фрагменты по смещению 0. Этот процесс повторяется для смещения – 1, 2, 3,… После того, как процедура кодирования закончена, фрагменты сохраняются на разные диски. Это можно изобразить следующим образом:

При выходе из строя одного или нескольких дисков, соответствующие потерянные фрагменты реконструируются и сохраняются на других дисках.
Теоретическая часть постепенно подходит к концу, будем надеяться, что базовый принцип кодирования и декодирования данных с использованием кодов Рида-Соломона теперь более или менее понятен. Если будет интерес к данной теме, то в следующих частях можно будет более подробно остановится на арифметике полей Галуа, реализациях алгоритма кодирования/декодирования на конкретных аппаратных платформах, поговорить про техники оптимизации.
UPD. Вынесенный из комментариев список литературы по теме (спасибо whitedruid):
— «Алгебраическая теория кодирования», Берлекэмп Э., 1971.
— «Теория кодов, исправляющих ошибки», Мак-Вильямс Ф., Слоэн Н.Дж., 1979.
— «Теория и практика кодов, контролирующих ошибки.», 1986.
— «Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение», Морелос-Сарагоса Р., 2005.
— «Кодирование с исправлением ошибок в системах цифровой связи», Кларк Дж., Кейн Дж., 1987.
— «Упаковки шаров, решетки и группы.», Конвей Дж.Н., Слоэн Н.Дж.А., 1990.

whitedruid: Книгу «Упаковка шаров, решетки и группы» сам прочёл относительно недавно — очень понравилось!
— «Введение в алгебраические коды» — лекции преподавателя МФТИ Юрия Львовича Сагаловича, оформленные в виде книги.
— «Коды Рида-Соломона с точки зрения обывателя» — написано простым языком.
— «Коды, исправляющие ошибки» — кратко, понятно и с картинками 🙂
— «Заметки по теории кодирования», А. Ромащенко, А. Румянцев, А. Шень, 2011 год. — своего рода «шпаргалка» — кратко, ёмко, однако требует некоторого уровня подготовки.
— Также нельзя обойти стороной семинары по «Теории кодирования», которые регулярно организуются сотрудниками «Институт проблем передачи информации им. А.А. Харкевича Российской академии наук», г. Москва. Далее — по ссылкам — можно найти много интересного по темам, связанным с математической теорией кодирования, поднимаются актуальные вопросы в рамках дисциплины. Например, про последовательное декодирование полярных и расширенных кодов Рида-Соломона. В поисковых же системах можно найти уже статьи автора.

Вы можете помочь и перевести немного средств на развитие сайта

Формальное описание

Коды Рида — Соломона являются важным частным случаем БЧХ-кода, корни порождающего полинома которого лежат в том же поле, над которым строится код ( m = 1 {\displaystyle m=1} ). Пусть α {\displaystyle \alpha } — элемент поля G F ( q ) {\displaystyle \textstyle GF(q)} порядка n {\displaystyle \textstyle n} . Если α {\displaystyle \alpha } — примитивный элемент, то его порядок равен q − 1 {\displaystyle q-1} , то есть α q − 1 = 1 , α i ≠ 1 , 0 < i < q − 1 {\displaystyle \alpha ^{q-1}=1,\quad \alpha ^{i}\neq 1,0<i<q-1} . Тогда нормированный полином g ( x ) {\displaystyle g(x)} минимальной степени над полем G F ( q ) {\displaystyle \textstyle GF(q)} , корнями которого являются d − 1 {\displaystyle d-1} подряд идущих степеней α l 0 , α l 0 + 1 , . . . , α l 0 + d − 2 {\displaystyle \alpha ^{l_{0}},\alpha ^{l_{0}+1},…,\alpha ^{l_{0}+d-2}} элемента α {\displaystyle \alpha } , является порождающим полиномом кода Рида — Соломона над полем G F ( q ) {\displaystyle \textstyle GF(q)} :

g ( x ) = ( x − α l 0 ) ( x − α l 0 + 1 ) … ( x − α l 0 + d − 2 ) {\displaystyle g(x)=(x-\alpha ^{l_{0}})(x-\alpha ^{l_{0}+1})\dots (x-\alpha ^{l_{0}+d-2})}

где l 0 {\displaystyle l_{0}} — некоторое целое число (в том числе 0 и 1), с помощью которого иногда удается упростить кодер. Обычно полагается l 0 = 1 {\displaystyle l_{0}=1} . Степень многочлена g ( x ) {\displaystyle \textstyle g(x)} равна d − 1 {\displaystyle d-1} .

Длина полученного кода n {\displaystyle n} , минимальное расстояние d {\displaystyle d} (минимальное расстояние d линейного кода является минимальным из всех расстояний Хемминга всех пар кодовых слов, см. Линейный код). Код содержит r = d − 1 = deg ⁡ ( g ( x ) ) {\displaystyle r=d-1=\deg(g(x))} проверочных символов, где deg ⁡ ( ) {\displaystyle \deg()} обозначает степень полинома; число информационных символов k = n − r = n − d + 1 {\displaystyle k=n-r=n-d+1} . Таким образом d = n − k + 1 {\displaystyle \textstyle d=n-k+1} и код Рида — Соломона является разделимым кодом с максимальным расстоянием (является оптимальным в смысле границы Синглтона).

Кодовый полином c ( x ) {\displaystyle c(x)} может быть получен из информационного полинома m ( x ) {\displaystyle m(x)} , deg ⁡ m ( x ) ⩽ k − 1 {\displaystyle \deg m(x)\leqslant k-1} , путём перемножения m ( x ) {\displaystyle m(x)} и g ( x ) {\displaystyle g(x)} :

c ( x ) = m ( x ) g ( x ) {\displaystyle c(x)=m(x)g(x)}

Свойства

Код Рида — Соломона над G F ( q m ) {\displaystyle \textstyle GF(q^{m})} , исправляющий t {\displaystyle t} ошибок, требует 2 t {\displaystyle 2t} проверочных символов и с его помощью исправляются произвольные пакеты ошибок длиной t {\displaystyle t} и меньше. Согласно теореме о границе Рейгера, коды Рида — Соломона являются оптимальными с точки зрения соотношения длины пакета и возможности исправления ошибок — используя 2 t {\displaystyle 2t} дополнительных проверочных символов исправляется t {\displaystyle t} ошибок (и менее).

Теорема (граница Рейгера). Каждый линейный блоковый код, исправляющий все пакеты длиной t {\displaystyle t} и менее, должен содержать, по меньшей мере, 2 t {\displaystyle 2t} проверочных символов.

Код, двойственный коду Рида — Соломона, есть также код Рида — Соломона. Двойственным кодом для циклического кода называется код, порожденный его проверочным многочленом.

Матрица G = {\displaystyle G=} порождает код Рида — Соломона тогда и только тогда когда любой минор матрицы P k ∗ ( n − k ) {\displaystyle P_{k*(n-k)}} отличен от нуля.

При выкалывании или укорочении кода Рида — Соломона снова получается код Рида — Соломона. Выкалывание — операция, состоящая в удалении одного проверочного символа. Длина n {\displaystyle n} кода уменьшается на единицу, размерность k {\displaystyle k} сохраняется. Расстояние кода d {\displaystyle d} должно уменьшиться на единицу, ибо в противном случае удаленный символ был бы бесполезен. Укорочение — фиксируем произвольный столбец ( n , k , d ) {\displaystyle (n,k,d)} кода и выбираем только те векторы, которые в данном столбце содержат 0. Это множество векторов образует подпространство.

Исправление многократных ошибок

Код Рида — Соломона является одним из наиболее мощных кодов, исправляющих многократные пакеты ошибок. Применяется в каналах, где пакеты ошибок могут образовываться столь часто, что их уже нельзя исправлять с помощью кодов, исправляющих одиночные ошибки.

( q m − 1 , q m − 1 − 2 t ) {\displaystyle (q^{m}-1,q^{m}-1-2t)}

Код Рида — Соломона над полем G F ( q m ) {\displaystyle \textstyle GF(q^{m})} с кодовым расстоянием d = 2 t + 1 {\displaystyle d=2t+1} можно рассматривать как ( ( q m − 1 ) m , ( q m − 1 − 2 t ) m ) {\displaystyle ((q^{m}-1)m,(q^{m}-1-2t)m)} -код над полем G F ( q ) {\displaystyle \textstyle GF(q)} , который может исправлять любую комбинацию ошибок, сосредоточенную в t {\displaystyle t} или меньшем числе блоков из m символов. Наибольшее число блоков длины m {\displaystyle m} , которые может затронуть пакет длины l i {\displaystyle l_{i}} , где l i ⩽ m t i − ( m − 1 ) {\displaystyle l_{i}\leqslant mt_{i}-(m-1)} , не превосходит t i {\displaystyle t_{i}} , поэтому код, который может исправить t {\displaystyle t} блоков ошибок, всегда может исправить и любую комбинацию из p {\displaystyle p} пакетов общей длины l {\displaystyle l} , если l + ( m − 1 ) ⩽ m t {\displaystyle l+(m-1)\leqslant mt} .

Практическая реализация

Кодирование с помощью кода Рида — Соломона может быть реализовано двумя способами: систематическим и несистематическим (см. , описание кодировщика).

При несистематическом кодировании информационное слово умножается на некий неприводимый полином в поле Галуа. Полученное закодированное слово полностью отличается от исходного и для извлечения информационного слова нужно выполнить операцию декодирования и уже потом можно проверить данные на содержание ошибок. Такое кодирование требует большие затраты ресурсов только на извлечение информационных данных, при этом они могут быть без ошибок.

Структура систематического кодового слова Рида — Соломона

При систематическом кодировании к информационному блоку из k {\displaystyle k} символов приписываются 2 t {\displaystyle 2t} проверочных символов, при вычислении каждого проверочного символа используются все k {\displaystyle k} символов исходного блока. В этом случае нет затрат ресурсов при извлечении исходного блока, если информационное слово не содержит ошибок, но кодировщик/декодировщик должен выполнить k ( n − k ) {\displaystyle k(n-k)} операций сложения и умножения для генерации проверочных символов. Кроме того, так как все операции проводятся в поле Галуа, то сами операции кодирования/декодирования требуют много ресурсов и времени. Быстрый алгоритм декодирования, основанный на быстром преобразовании Фурье, выполняется за время порядка O ( l n ( n ) 2 ) {\displaystyle O({ln({n})}^{2})} .

Кодирование

При операции кодирования информационный полином умножается на порождающий многочлен. Умножение исходного слова S {\displaystyle S} длины k {\displaystyle k} на неприводимый полином при систематическом кодировании можно выполнить следующим образом:

• К исходному слову приписываются 2 t {\displaystyle 2t} нулей, получается полином T = S x 2 t {\displaystyle \textstyle T=Sx^{2t}} .
• Этот полином делится на порождающий полином G {\displaystyle G} , находится остаток R {\displaystyle R} , S x 2 t = Q G + R {\displaystyle \textstyle Sx^{2t}=QG+R} , где Q {\displaystyle Q} — частное.
• Этот остаток и будет корректирующим кодом Рида — Соломона, он приписывается к исходному блоку символов. Полученное кодовое слово C = S x 2 t + R {\displaystyle \textstyle C=Sx^{2t}+R} .

Кодировщик строится из сдвиговых регистров, сумматоров и умножителей. Сдвиговый регистр состоит из ячеек памяти, в каждой из которых находится один элемент поля Галуа.

Существует и другая процедура кодирования (более практичная и простая). Положим a i ∈ G F ( q ) , ( i = 1 , 2 , … , k − 1 ) , α ∈ G F ( q ) {\displaystyle a_{i}\in GF(q),(i=1,2,\ldots ,k-1),\alpha \in GF(q)} — примитивный элемент поля G F ( q ) {\displaystyle GF(q)} , и пусть a = ( a 0 , a 1 , … , a k − 1 ) {\displaystyle a=(a_{0},a_{1},\ldots ,a_{k-1})} — вектор информационных символов, а значит a ( x ) = a 0 + a 1 x + … + a k − 1 x k − 1 {\displaystyle a(x)=a_{0}+a_{1}x+\ldots +a_{k-1}x^{k-1}} — информационный многочлен. Тогда вектор u = ( a ( 1 ) , a ( α ) , … , a ( α q − 2 ) ) {\displaystyle u=(a(1),a(\alpha ),\ldots ,a(\alpha ^{q-2}))} есть вектор кода Рида — Соломона, соответствующий информационному вектору a {\displaystyle a} . Этот способ кодирования показывает, что для кода РС вообще не нужно знать порождающего многочлена и порождающей матрицы кода, достаточно знать разложение поля G F ( q ) {\displaystyle GF(q)} по примитивному элементу α {\displaystyle \alpha } и размерность кода k {\displaystyle k} (длина кода в этом случае определяется как n = q − 1 {\displaystyle n=q-1} ). Все дело в том, что за разностью n − k {\displaystyle n-k} полностью скрывается порождающий многочлен g ( x ) {\displaystyle g(x)} и кодовое расстояние.

Декодирование

Декодировщик, работающий по авторегрессивному спектральному методу декодирования, последовательно выполняет следующие действия:

• Вычисляет синдром ошибки
• Строит полином ошибки
• Находит корни данного полинома
• Определяет характер ошибки
• Исправляет ошибки

Вычисление синдрома ошибки

Вычисление синдрома ошибки выполняется синдромным декодером, который делит кодовое слово на порождающий многочлен. Если при делении возникает остаток, то в слове есть ошибка. Остаток от деления является синдромом ошибки.

Построение полинома ошибки

Вычисленный синдром ошибки не указывает на положение ошибок. Степень полинома синдрома равна 2 t {\displaystyle 2t} , что много меньше степени кодового слова n {\displaystyle n} . Для получения соответствия между ошибкой и её положением в сообщении строится полином ошибок. Полином ошибок реализуется с помощью алгоритма Берлекэмпа — Месси, либо с помощью алгоритма Евклида. Алгоритм Евклида имеет простую реализацию, но требует больших затрат ресурсов. Поэтому чаще применяется более сложный, но менее затратоемкий алгоритм Берлекэмпа — Месси. Коэффициенты найденного полинома непосредственно соответствуют коэффициентам ошибочных символов в кодовом слове.

Нахождение корней

На этом этапе ищутся корни полинома ошибки, определяющие положение искаженных символов в кодовом слове. Реализуется с помощью процедуры Ченя, равносильной полному перебору. В полином ошибок последовательно подставляются все возможные значения, когда полином обращается в ноль — корни найдены.

Определение характера ошибки и её исправление

Основная статья: Код Боуза — Чоудхури — Хоквингема § Методы декодирования

По синдрому ошибки и найденным корням полинома с помощью алгоритма Форни определяется характер ошибки и строится маска искаженных символов. Однако для кодов РС существует более простой способ отыскания характера ошибок. Как показано в для кодов РС с произвольным множеством 2 t d {\displaystyle 2t_{d}} последовательных нулей α b , α b + 1 , … , α b + δ , δ = 2 t d − 1 {\displaystyle \alpha ^{b},\alpha ^{b+1},\ldots ,\alpha ^{b+\delta },\delta =2t_{d}-1}

e j l = ( α j l ) 2 − b Λ ( α − j l ) σ ′ ( α − j l ) ( ∗ ) {\displaystyle e_{j_{l}}={\frac {(\alpha ^{j_{l}})^{2-b}\Lambda (\alpha ^{-j_{l}})}{\sigma ‘(\alpha ^{-j_{l}})}}\quad \quad \quad (*)}

где σ ′ ( x ) {\displaystyle \sigma ‘(x)} формальная производная по x {\displaystyle x} многочлена локаторов ошибок σ ( x ) {\displaystyle \sigma (x)} ,а Λ ( x ) = σ ( x ) S ( x ) mod x 2 t d + 1 {\displaystyle \Lambda (x)=\sigma (x)S(x)\mod x^{2t_{d}+1}}

Далее после того как маска найдена, она накладывается на кодовое слово с помощью операции XOR и искаженные символы восстанавливаются. После этого отбрасываются проверочные символы и получается восстановленное информационное слово.

Алгоритм Судана

В данное время стали применяться принципиально новые методы декодирования, например, алгоритм, предложенный в 1997 году Мадху Суданом.

Удлинение кодов РС

Удлинение кодов РС — это процедура, при которой увеличивается длина и расстояние кода (при этом код ещё находится на границе Синглтона и алфавит кода не изменяется), а количество информационных символов кода не изменяется. Такая процедура увеличивает корректирующую способность кода. Рассмотрим удлинение кода РС на один символ. Пусть υ = ( c 0 , c 1 , … , c q − 2 ) {\displaystyle \upsilon =(c_{0},c_{1},\ldots ,c_{q-2})} — вектор кода РС, порождающий многочлен которого есть g ( x ) = ( x − α ) ( x − α 2 ) … ( x − α d − 1 ) , deg ⁡ g ( x ) = d − 1 = r = n − k , n = q − 1 {\displaystyle g(x)=(x-\alpha )(x-\alpha ^{2})\ldots (x-\alpha ^{d-1}),\deg g(x)=d-1=r=n-k,n=q-1} . Пусть теперь c q − 1 = − ∑ i = 1 q − 2 c i {\displaystyle c_{q-1}=-\sum _{i=1}^{q-2}c_{i}} . Покажем, что добавление к вектору υ {\displaystyle \upsilon } символа c q − 1 {\displaystyle c_{q-1}} увеличит его вес до d + 1 {\displaystyle d+1} ,если c q − 1 ≠ 0 {\displaystyle c_{q-1}\neq 0} . Многочлен, соответствующий вектору кода, можно расписать как υ ( x ) = g ( x ) ∗ z ( x ) {\displaystyle \upsilon (x)=g(x)*z(x)} , но тогда с учётом выражения для c q − 1 {\displaystyle c_{q-1}} получим υ ( 1 ) = g ( 1 ) z ( 1 ) = − c q − 1 {\displaystyle \upsilon (1)=g(1)z(1)=-c_{q-1}} . g ( 1 ) ≠ 0 {\displaystyle g(1)\neq 0} , так как 1 не принадлежит списку корней порождающего многочлена. Но и z ( 1 ) ≠ 0 {\displaystyle z(1)\neq 0} , так как в этом случае ( x − 1 ) g ( x ) | υ ( x ) {\displaystyle (x-1)g(x)|\upsilon (x)} ,что увеличило бы расстояние кода вопреки условию, это значит что c q − 1 ≠ 0 {\displaystyle c_{q-1}\neq 0} и вес кода увеличился, за счёт добавления нового символа c q − 1 {\displaystyle c_{q-1}} . Новые параметры кода n 1 = n + 1 , k 1 = k , d 1 = d + 1 {\displaystyle n_{1}=n+1,k_{1}=k,d_{1}=d+1} , удлиненный вектор v 1 = ( c 0 , c 1 , … , c q − 2 , c q − 1 ) {\displaystyle v_{1}=(c_{0},c_{1},\ldots ,c_{q-2},c_{q-1})} . Проверочная матрица не удлиненного кода имеет вид

Тогда проверочная матрица, удлиненного на один символ РС кода будет

Применение

Сразу после появления (60-е годы 20-го века) коды Рида — Соломона стали применяться в качестве внешних кодов в каскадных конструкциях, использующихся в спутниковой связи. В подобных конструкциях q {\displaystyle q} -е символы РС (их может быть несколько) кодируются внутренними сверточными кодами. На приемном конце эти символы декодируются мягким алгоритмом Витерби (эффективный в каналах с АБГШ) . Такой декодер будет исправлять одиночные ошибки в q-ичных символах, когда же возникнут пакетные ошибки и некоторые пакеты q-ичных символов будут декодированы неправильно, тогда внешний декодер Рида — Соломона исправит пакеты этих ошибок. Таким образом будет достигнута требуемая надежность передачи информации ().

В настоящий момент коды Рида — Соломона имеют очень широкую область применения благодаря их способности находить и исправлять многократные пакеты ошибок.

Запись и хранение информации

Код Рида — Соломона используется при записи и чтении в контроллерах оперативной памяти, при архивировании данных, записи информации на жесткие диски (ECC), записи на CD/DVD диски. Даже если поврежден значительный объем информации, испорчено несколько секторов дискового носителя, то коды Рида — Соломона позволяют восстановить большую часть потерянной информации. Также используется при записи на такие носители, как магнитные ленты и штрихкоды.

Запись на CD-ROM

Возможные ошибки при чтении с диска появляются уже на этапе производства диска, так как сделать идеальный диск при современных технологиях невозможно. Также ошибки могут быть вызваны царапинами на поверхности диска, пылью и т. д. Поэтому при изготовлении читаемого компакт-диска используется система коррекции CIRC (Cross Interleaved Reed Solomon Code). Эта коррекция реализована во всех устройствах, позволяющих считывать данные с CD дисков, в виде чипа с прошивкой firmware. Нахождение и коррекция ошибок основана на избыточности и перемежении (redundancy & interleaving). Избыточность примерно 25 % от исходной информации.

При записи на аудиокомпакт-диски используется стандарт Red Book. Коррекция ошибок происходит на двух уровнях, C1 и C2. При кодировании на первом этапе происходит добавление проверочных символов к исходным данным, на втором этапе информация снова кодируется. Кроме кодирования осуществляется также перемешивание (перемежение) байтов, чтобы при коррекции блоки ошибок распались на отдельные биты, которые легче исправляются. На первом уровне обнаруживаются и исправляются ошибочные блоки длиной один и два байта (один и два ошибочных символа, соответственно). Ошибочные блоки длиной три байта обнаруживаются и передаются на следующий уровень. На втором уровне обнаруживаются и исправляются ошибочные блоки, возникшие в C2, длиной 1 и 2 байта. Обнаружение трех ошибочных символов является фатальной ошибкой и не может быть исправлено.

Беспроводная и мобильная связь

Этот алгоритм кодирования используется при передаче данных по сетям WiMAX, в оптических линиях связи, в спутниковой и радиорелейной связи. Метод прямой коррекции ошибок в проходящем трафике (Forward Error Correction, FEC) основывается на кодах Рида — Соломона.

Примеры кодирования

16-ричный (15,11) код Рида — Соломона

Пусть t = 2 , l 0 = 1 {\displaystyle t=2,l_{0}=1} . Тогда

Степень g ( x ) {\displaystyle g(x)} равна 4, n − k = 4 {\displaystyle n-k=4} и k = 11 {\displaystyle k=11} . Каждому элементу поля G F ( 16 ) {\displaystyle \mathrm {GF} (16)} можно сопоставить 4 бита. Информационный многочлен является последовательностью 11 символов из G F ( 16 ) {\displaystyle \mathrm {GF} (16)} , что эквивалентно 44 битам, а все кодовое слово является набором из 60 бит.

8-ричный (7,3) код Рида — Соломона

Пусть t = 2 , l 0 = 4 {\displaystyle t=2,l_{0}=4} . Тогда

Пусть информационный многочлен имеет вид

m ( x ) = α 4 x 2 + x + α 3 {\displaystyle m(x)=\alpha ^{4}x^{2}+x+\alpha ^{3}}

Кодовое слово несистематического кода запишется в виде

что представляет собой последовательность семи восьмеричных символов.

Альтернативный метод кодирования 9-ричного (8,4) кода Рида — Соломона

Построим поле Галуа G F ( 3 2 ) {\displaystyle GF(3^{2})} по модулю многочлена x 2 + x + 2 {\displaystyle x^{2}+x+2} .Пусть α {\displaystyle \alpha } его корень, тогда α 2 + α + 2 = 0 {\displaystyle \alpha ^{2}+\alpha +2=0} , таблица поля имеет вид:

Пусть информационный многочлен a ( x ) = 1 + α x + α 2 x 2 + α 3 x 3 {\displaystyle a(x)=1+\alpha x+\alpha ^{2}x^{2}+\alpha ^{3}x^{3}} , далее производя соответствующие вычисления над построенным полем получим a ( 1 ) = α 2 , a ( α ) = 0 , a ( α 2 ) = α 6 , a ( α 3 ) = 0 , a ( α 4 ) = α 5 , a ( α 5 ) = 0 , a ( α 6 ) = α 7 , a ( α 7 ) = 1 {\displaystyle a(1)=\alpha ^{2},a(\alpha )=0,a(\alpha ^{2})=\alpha ^{6},a(\alpha ^{3})=0,a(\alpha ^{4})=\alpha ^{5},a(\alpha ^{5})=0,a(\alpha ^{6})=\alpha ^{7},a(\alpha ^{7})=1}

В итоге построен вектор кода РС с параметрами n = 8 , k = 4 , d = 5 {\displaystyle n=8,k=4,d=5} .На этом кодирование законченно. Заметим, что при этом способе нам не потребовался порождающий многочлен кода.

Примеры декодирования

Пусть поле G F ( 2 3 ) {\displaystyle GF(2^{3})} генерируется примитивным элементом, неприводимый многочлен которого p ( x ) = x 3 + x + 1 {\displaystyle p(x)=x^{3}+x+1} . Тогда p ( α ) = α 3 + α + 1 = 0 {\displaystyle p(\alpha )=\alpha ^{3}+\alpha +1=0} . Пусть b = 0 , t d = 2 {\displaystyle b=0,t_{d}=2} . Тогда порождающий многочлен кода РС равен g ( x ) = ( x + 1 ) ( x + α ) ( x + α 2 ) ( x + α 3 ) = x 4 + α 2 x 3 + α 5 x 2 + α 5 x 2 + α 6 {\displaystyle g(x)=(x+1)(x+\alpha )(x+\alpha ^{2})(x+\alpha ^{3})=x^{4}+\alpha ^{2}x^{3}+\alpha ^{5}x^{2}+\alpha ^{5}x^{2}+\alpha ^{6}} . Пусть теперь принят многочлен r ( x ) = α x 2 + α 5 x 4 {\displaystyle r(x)=\alpha x^{2}+\alpha ^{5}x^{4}} . Тогда S 1 = r ( 1 ) = α + α 5 = α 6 , S 2 = r ( α ) = α 5 , S 3 = α , S 4 = α {\displaystyle S_{1}=r(1)=\alpha +\alpha ^{5}=\alpha ^{6},S_{2}=r(\alpha )=\alpha ^{5},S_{3}=\alpha ,S_{4}=\alpha } . Тогда ключевая система уравнений получается в виде

Теперь рассмотрим Евклидов алгоритм решения этой системы уравнений.

• Начальные условия:

• i = 2 {\displaystyle i=2}

• i = 3 {\displaystyle i=3}

Алгоритм останавливается, так как deg ⁡ = 2 = t d {\displaystyle \deg=2=t_{d}} отсюда следует, что σ ( x ) = α 3 + α 4 x + α 2 x 2 {\displaystyle \sigma (x)=\alpha ^{3}+\alpha ^{4}x+\alpha ^{2}x^{2}}

Далее полный перебор по алгоритму Чени выдает нам позиции ошибок, это j 1 = 2 , j 2 = 4 {\displaystyle j_{1}=2,\quad j_{2}=4} .Потом по формуле ( ∗ ) {\displaystyle (*)} получаем что e 2 = α , e 4 = α {\displaystyle e_{2}=\alpha ,e_{4}=\alpha }

Таким образом декодированный вектор c ( x ) = r ( x ) + e ( x ) = 0 {\displaystyle c(x)=r(x)+e(x)=0} . Декодирование завершено, исправлены две ошибки.

> Применение

• Код Рида — Соломона используется в некоторых прикладных программах в области хранения данных, например в RAID 6;

Коды Рида-Соломона. Простой пример

Благодаря кодам Рида-Соломона можно прочитать компакт-диск с множеством царапин, либо передать информацию в условиях связи с большим количеством помех. В среднем для компакт-диска избыточность кода (т.е. количество дополнительных символов, благодаря которым информацию можно восстанавливать) составляет примерно 25%. Восстановить при этом можно количество данных, равное половине избыточных. Если емкость диска 700 Мб, то, получается, теоретически можно восстановить до 87,5 Мб из 700. При этом нам не обязательно знать, какой именно символ передан с ошибкой. Также стоит отметить, что вместе с кодированием используется перемежевание, когда байты разных блоков перемешиваются в определенном порядке, что в результате позволяет читать диски с обширными повреждениями, локализированными близко друг к другу (например, глубокие царапины), так как после операции, обратной перемежеванию, обширное повреждение оборачивается единичными ошибками во множестве блоков кода, которые поддаются восстановлению.

Давайте возьмем простой пример и попробуем пройти весь путь – от кодирования до получения исходных данных на приемнике. Пусть нам нужно передать кодовое слово С, состоящее из двух чисел – 3 и 1 именно в такой последовательности, т.е. нам нужно передать вектор С=(3,1). Допустим, мы хотим исправить максимум две ошибки, не зная точно, где они могут появиться. Для этого нужно взять 2*2=4 избыточных символа. Запишем их нулями в нашем слове, т.е. С теперь равно (3,1,0,0,0,0). Далее необходимо немного разобраться с математическими особенностями.

Многие знают романтическую историю о молодом человеке, который прожил всего 20 лет и однажды ночью написал свою математическую теорию, а утром был убит на дуэли. Это Эварист Галуа. Также он несколько раз пытался поступить в университеты, однако экзаменаторы не понимали его решений, и он проваливал экзамены. Приходилось ему учиться самостоятельно. Ни Гаусс, ни Пуассон, которым он послал свои работы, также не поняли их, однако его теория отлично пригодилась в 60-х годах ХХ-го века, и активно используется в наше время как для теоретических вычислений в новых разделах математики, так и на практике.
Мы будем использовать довольно простые выводы, следующие из его теории групп. Основная идея – есть конечное (а не бесконечное) количество чисел, называемое полем, с помощью которых можно проводить все известные математические операции. Количество чисел в поле должно являться простым числом в любой натуральной степени, однако в случае простых кодов Рида-Соломона, рассматриваемых здесь, размерность поля — простое число в степени 1. В расширенных кодах Рида-Соломона степень более 1.
Например, для поля Галуа размерности 7, т.е. GF(7), все математические операции будут происходить с числами 0,1,2,3,4,5,6.
Пример сложения: 1+2=3; 4+5=9 mod 7=2. Сложение в полях Галуа представляет собой сложение по модулю. Вычитание и умножение также делается по модулю.
Пример деления: 5/6 = 30/36 = 30/(36 mod 7) = 30/1 = 30 = 30 mod 7 = 2.
Возведение степень происходит аналогично умножению.

Полезное свойство обнаруживается в полях Галуа при возведении в степень. Как можно заметить, если возвести в степень числа 3 либо 5 в выбранном поле Галуа GF(7), в строке присутствуют все элементы текущего поля Галуа кроме 0. Такие числа называются примитивными элементами. В кодах Рида-Соломона обычно используется самый большой примитивный элемент выбранного поля Галуа. Для GF(7) он равен 5.
Можно отметить, что числа в полях Галуа – это вместе с тем и абстракции, которые имеют более тесную связь между собой, чем привычные нам числа.

Интерполяция

Как многие знают еще со школьного курса, интерполяция – это нахождение многочлена минимальной степени в данном наборе точек. Например, есть три точки и три значения какой-то функции в этих точках. Можно найти функцию, которая удовлетворяет таким входным данные. Например, это очень просто сделать с помощью преобразования Лагранжа. После того, как функция найдена, можно построить еще несколько точек, и эти точки будут связаны с тремя исходными точками. Формирование избыточных символов при кодировании – это операция, похожая на интерполяцию.

Обратное дискретное преобразование Фурье (IDFT)

Преобразование Фурье, наряду с теорией групп Галуа – это еще одна вершина математической мысли, которая в сегодняшнее время используется во множестве областей. Некоторые даже считают, что преобразование Фурье описывает один из фундаментальных законов Вселенной. Основная суть: любой непериодический сигнал конечной протяженности можно представить в виде суммы синусоид разных частот и фаз, потом по ним можно заново построить исходный сигнал. Однако это не единственное описание. Числа в полях Галуа напоминают упомянутые разные частоты синусоид, так что преобразование Фурье можно использовать и для них.
Дискретное преобразование Фурье – это формула преобразования Фурье для дискретных значений. Преобразование имеет два направления – прямое и обратное. Обратное преобразование проще математически, поэтому давайте закодируем рассматриваемое слово С=(3,1,0,0,0,0) с помощью него. Первые два символа – информация, последние четыре – избыточные и всегда равны 0.
Запишем кодовое слово С в виде полинома: С=3*х0+1*х1 + 0*х2 +… = 3+х. Как поле Галуа возьмем упомянутое GF(7), где примитивный элемент = 5. Делая IDFT, находятся значения полинома С для примитивного элемента z разных степеней. Формула IDFT: cj=C(zj). То есть, находим значения функции С(zj), где j – элементы поля Галуа GF(7). Мы рассчитываем до j=N-2=7-2=5 степени. Посмотрев на таблицу степеней, можно догадаться, почему: в шестой степени значение снова 1, т.е. повторяется, вследствие чего потом невозможно было бы определить, в какую степень возводили – в 6ю или 0ю.
с0 = С(z0) = 3 + 1* z0 = 3 + 1* 50 = 4
с1 = С(z1) = 3 + 1* z1 = 8 = 1
с2 = С(z2) = 3 + 1* z2 = 0
…
Таким образом С(3,1,0,0,0,0) => с(4,1,0,2,5,6).
Мы передаем слово с(4,1,0,2,5,6).

Ошибка

Ошибка представляет собой еще одно слово, которое суммируется с передаваемым. Например, ошибка f=(0,0,0,2,0,6). Если сделать с + f, то получим сf(4,1,0,4,5,5).

Прямое преобразование Фурье (DFT). Декодирование. Синдром

На приемнике мы получили слово с+f = сf(4,1,0,4,5,5). Как проверить, были ли ошибки при передаче? Известно, что мы кодировали информацию с помощью IDFT в GF(7). DFT (дискретное преобразование Фурье) – это преобразование, обратное IDFT. Проделав его, можно получить исходную информацию и четыре нуля (т.е. С(3,1,0,0,0,0)), в случае, если ошибок не было. Если же ошибки были, то вместо этих четырех нулей будут другие цифры. Проделаем DFT для сf и проверим, есть ли ошибки. Формула DFT: Сk=N-1*c(z-kj). По-прежнему используется примитивный элемент z=5 поля GF(7).
C0 = c(5-0*j)/6 = (4*5-0*0 + 1*5-1*0 + 0*5-2*0 + 4*5-3*0 + 5*5-4*0 + 5*5-5*0)/6 = (4 + 1 + 4 + 0 + 5 + 5)/6 = 19/6 = 5/6 = 30/36 = 30 = 2;
C1 = c(5-1*j)/6 = (4*5-0*1 + 1*5-1*1 + 0*5-2*1 + 4*5-3*1 + 5*5-4*1 + 5*5-5*1)/6 = (4 + 3/15 + 24/750 + 20/2500 + 25/15625)/6 = (4 + 3 + 24 + 20 + 25)/6 = 76/6 = 456/36 = 456 = 1;
C2 = c(5-2*j)/6 = (4*5-0*2 + 1*5-1*2 + 0*5-2*2 + 4*5-3*2 + 5*5-4*2 + 5*5-5*2)/6 = (4 + 2 + 4 + 10 + 20)/6 = 40/6 = 240/36 = 240 = 2;
…
сf(4,1,0,4,5,5) => Cf(2,1,2,1,0,5). Выделенные символы были бы нулями, если бы ошибки не было. Теперь видно, что ошибка была. В данном случае символы 2,1,0,5 называются синдромом ошибки.

Алгоритм Берлекампа-Месси для вычисления позиции ошибки

Чтобы исправить ошибку, нужно знать, какие именно символы были переданы с ошибкой. На этом этапе вычисляется, где находятся ошибочные символы, сколько было ошибок, а также можно ли исправить такое количество ошибок.
Алгоритм Берлекампа-Месси занимается поиском полинома, который, при перемножении на специальную матрицу, подготовленную из чисел синдрома (пример далее), отдаст нулевой вектор. Доказательство алгоритма показывает, что корни этого полинома содержат информацию о позиции символов с ошибками в полученном кодовом слове.
Так как максимальное количество ошибок для рассматриваемого случая может быть 2, напишем формулу искомого полинома в матричном виде для двух ошибок (полином степени 2): Г = .
Теперь запишем синдром (2,1,0,5) в формате матрицы Тёплица. Если вы посмотрите на синдром и на полученную матрицу, вы сразу заметите принцип создания такой матрицы. Размерность матрицы обусловлена полиномом Г, обозначенным выше.

Уравнение, которое нужно решить:

Элементы под знаками вопроса не влияют на результат. Необходимо найти Г1 и Г2, они отвечают за позиции ошибок. Мы постепенно будем увеличивать размерность, с которой работаем. Начинаем с 1 и с нижнего левого края матрицы (отмечено зеленым) при минимальной размерности 1х1.

Увеличиваем размерность. Предположим, что ошибки в позиции Г1 у нас нет. Тогда Г1 = 0.

Мы должны получить справа, или, как минимум, один 0 на первом месте, чтобы повысить размерность вычислений, однако на первом месте стоит 1. Мы можем подобрать такое значение для Г1 (которое сейчас 0), чтобы справа получить необходимый 0. Процесс подбора значения Г1 в алгоритме оптимизирован. Запишем два уравнения, рассмотренных ваше, еще раз, а также выведем третье уравнение, которым вычисляется Г1. Цветами показано, что куда идет.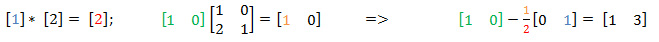

Т.е. Г1 = 3. Напоминаю, что подсчет идет в GF(7). Также стоит отметить, что значение Г1 временное. Во время расчетов Г2 оно может поменяться. Считаем заново правую часть: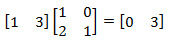

Получили 0 справа, теперь повышаем размерность. Предполагаем по аналогии, что Г2 = 0. Используем найденный Г1=3.

Первым делом вместо тройки справа нужно получить 0. Действия соответствуют предыдущим. Далее подбор значения Г2.

Запишем новое значение Г2=2 в основное уравнение и опять попробуем найти значения справа: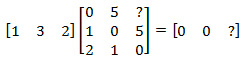

Задача на данном шаге была получить только первый ноль, однако волей случая второй элемент матрицы также оказался нулем, т.е. задача решена. Если бы он не был нулем, мы бы еще раз делали подбор значений (на этот раз и для Г1, и для Г2), повысив размерность подбора. Если вы заинтересовались данным алгоритмом, вот еще два примера.
Итак, Г1 = 3, Г2 = 2. Ненулевые значения для Г1 и Г2 показывает, что было 2 ошибки. Запишем матрицу Г в виде полинома: Г(z) = 1 + 3x + 2×2. Корни с учетом степеней примитивного элемента, в которых результат получается 0:
Г(53) = 1 + 3*6 + 2*62 = 91 = 13*7 = 0.
Г(55) = 1 + 3*3 + 2*32 = 28 = 0.
Это означает, что ошибки в позициях 3 и 5.
Аналогично можно найти остальные значения, чтобы убедиться, что они не дадут нули:
Г=>г(zj) = (3,5,5,0,4,0). Как вы могли заметить, снова используется IDFT в GF(7).

Исправление ошибок методом Форни

На предыдущем этапе вычислялись позиции ошибок, теперь осталось найти верные значения. Полином, описывающий позиции ошибок: Г(z) = 1 + 3x + 2×2. Запишем его в нормализированном виде, умножив на 4 и воспользовавшись свойствами GF(7): Г(z) = x2 + 5x + 4.
Метод Форни основан на интерполяции Лагранжа и использует полиномы, которыми мы оперировали в алгоритме Берлекампа-Месси.
В методе дополнительно рассчитываются те символы, которые стоят на местах, не относящихся к синдрому. Это те позиции, которые соответствуют реальным значениям, однако для них рассчитываются другие значения, которые получаются из свертки синдрома ошибки и полинома Г. Эти вычисленные новые значения вместе с синдромом формируют маску ошибки. Далее выполняется IDFT и результат представляет собой непосредственно ошибку, которая ранее суммировалась с передаваемым кодовым словом. Она вычитается из полученного слова и мы получаем первоначальное переданное слово. Затем выполняем DFT для переданного кодового слова и получаем, наконец, информацию. Далее — как это происходит в контексте рассматриваемого примера.
Запишем вектор ошибки F (последние 4 символа — синдром, который мы постоянно используем, два знака вопроса — на местах информационных символов, это маска ошибки) и обозначим каждый символ буквой:

Символы полинома локатора ошибки Г(z) = x2 + 5x + 4 обозначим так: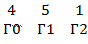
Перемножение полинома Г на матрицу Тёплица в предыдущем параграфе было, по сути, операцией циклической свертки: если расписать линейные уравнения, которые получаются из матричного, можно увидеть, что значения, которые берутся из синдрома (значения матрицы Тёплица), от уравнения к уравнению просто меняются местами, двигаясь последовательно в определенную сторону, а это и называется сверткой. Я специально разместил полиномы F и Г друг над другом в начале этого абзаца, чтобы можно было делать свертки (перемножать поэлементно в определенном порядке), двигая полиномы визуально. Раскрывая матричное уравнение из предыдущего параграфа и используя обозначения для полиномов F и Г, введенные только что:
Г0*F4 + Г1*F3 + Г2*F2 = 0
Г0*F5 + Г1*F4 + Г2*F3 = 0
Ранее свертка производилась только для синдрома, в методе Форни нужно сделать свертки для F0 и F1, а после найти их значения:
Г0*F3 + Г1*F2 + Г2*F1 = 0
Г0*F2 + Г1*F1 + Г2*F0 = 0
F0 = -Г0*F3 – Г1*F2 = 0
F1 = -Г0*F2 – Г1*F1 = 6
То есть F = (6,0,2,1,0,5). Проводим IDFT, так как ошибка суммировалась со словом, которое было в кодированном IDFT виде: f = (0,0,0,2,0,6).
Вычитаем ошибку f из полученного кодового слова cf: (4,1,0,4,5,5) — (0,0,0,2,0,6) = с(4,1,0,2,5,6)
Сделаем DFT для этого слова: с(4,1,0,2,5,6) => С=(3,1,0,0,0,0). А вот и наши символы 3 и 1, которые нужно было передать.

Заключение

Обычно используются расширенные коды Рида-Соломона, то есть поле Галуа представляет собой степень двойки (GF(2m)), например кодирование байтов информации. Алгоритмы работы похожи на те, что разобраны в этой статье.
Есть множество разновидностей алгоритма в зависимости от областей применения, а также в зависимости от возраста каждой конкретной разновидности и от компании-разработчика. Чем алгоритм моложе, тем он сложнее.
Также много устройств используют готовые таблицы ошибок, рассчитанные заранее. В условиях использования арифметики Галуа получается конечное количество возможных ошибок. Это свойство и используется для уменьшения количества расчетов. Здесь в случае, если синдром получается ненулевой, он просто сравнивается с таблицей возможных ошибочных синдромов.
Курс теории кодирования для многих часто является одним из самых сложных. Буду рад, если данная статья кому-нибудь поможет разобраться в данной теме быстрее.